【题目】执行两次如图所示的程序框图，若第一次输入的x值为7，第二次输入的x值为9，则第一次，第二次输出的a值分别为（ ）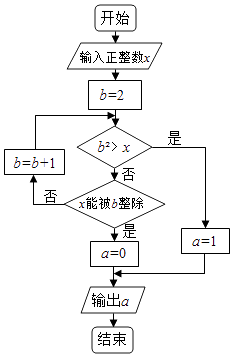
A.0，0
B.1，1
C.0，1
D.1，0
【答案】D
【解析】解：当输入的x值为7时，
第一次，不满足b2＞x，也不满足x能被b整数，故b=3；
第二次，满足b2＞x，故输出a=1；
当输入的x值为9时，
第一次，不满足b2＞x，也不满足x能被b整数，故b=3；
第二次，不满足b2＞x，但满足x能被b整数，故输出a=0
故选：D
【考点精析】解答此题的关键在于理解算法的条件结构的相关知识，掌握条件P是否成立而选择执行A框或B框．无论P条件是否成立，只能执行A框或B框之一，不可能同时执行A框和B框，也不可能A框、B框都不执行．一个判断结构可以有多个判断框，以及对算法的循环结构的理解，了解在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，循环结构可细分为两类：当型循环结构和直到型循环结构．
科目：高中数学 来源： 题型：
【题目】如图，平面中两条直线
和
相交于点O，对于平面上任意一点M，若x，y分别是M到直线和的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（p，q）的点有且只有2个；
③若pq≠0则“距离坐标”为（p，q）的点有且只有4个．
上述命题中，正确命题的是______．（写出所有正确命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校对校园进行绿化，移栽香樟和桂花两种大树各2株，若香樟的成活率为
，桂花的成活率为
，假设每棵树成活与否是相互独立的.求：
（Ⅰ）两种树各成活一株的概率；
（Ⅱ）设ξ表示两种树成活的总株数，求ξ的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】汕头某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题：(1)引进该设备多少年后,收回成本并开始盈利？(2)引进该设备若干年后,有两种处理方案：第一种：年平均盈利达到最大值时,以26万元的价格卖出；第二种：盈利总额达到最大值时,以8万元的价格卖出.问哪种方案较为合算？并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知0＜a＜b，且a+b=1，则下列不等式中正确的是（ ）
A.log2a＞0
B.2a﹣b＜ 
C.log2a+log2b＜﹣2
D.2（ 
+ 
）＜
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
