
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上. 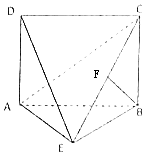
(1)求证:AE⊥BE;
(2)求三棱锥C﹣ADE的体积.
【答案】
(1)证明:∵DA⊥平面ABE,BC∥DA,
∴BC⊥平面ABE,
∵AE平面ABE,∴AE⊥BC,
∵BF⊥平面ACE于点F,AE平面ACE,
∴AE⊥BF,
∵BC∩BF=B,
BC平面BEC,BF平面BEC,∴AE⊥平面BEC,
∵BE平面BEC,∴AE⊥BE
(2)解:作EH⊥AB,
∵DA⊥平面ABE,EH平面ABE,∴AD⊥EH,
AD∩AB=A,AD平面ABCD,AB平面ABCD,
∴EH⊥平面ABCD,
由(1)得AE⊥BE,AE=EB=BC=2,
AB=2 ![]() ,EH=
,EH= ![]() ,
,
∴三棱锥C﹣ADE的体积VC﹣ADE=VE﹣ACD= ![]() =
= ![]() =
= ![]() .
.

【解析】(1)推导出BC⊥平面ABE,从而AE⊥BC,再求出AE⊥BF,从而AE⊥平面BEC,由此能证明AE⊥BE.(2)作EH⊥AB,三棱锥C﹣ADE的体积VC﹣ADE=VE﹣ACD , 由此能求出结果.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 , n∈N* , 令cn= ![]() ,n∈N* , 求数列{cncn+1}的前n项和Sn .
,n∈N* , 求数列{cncn+1}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是岁. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本,(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出如下频率分布直方图.
的分组作出如下频率分布直方图.
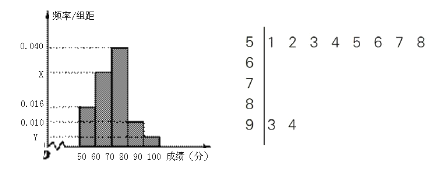
(1)由如下茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据)提供的信息,求样本容量
的数据)提供的信息,求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com