
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

(1)在棱![]() 上求一点
上求一点![]() ,使
,使![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
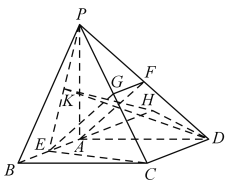
(1)分别取PD,PC的中点F,G,由三角形中位线定理及平行公理可得四边形AEGF为平行四边形,得AF∥EG,由线面平行的判定可得AF∥平面PEC,则PD的中点F即为所求;
(2)由已知可得∠CPE即为PC与平面PAB所成的角,求解直角三角形得到PA=2,过D作BA的延长线的垂线,垂足为H,过H作PE的垂线,垂足为K,连接KD,可得∠DKH即为所求的二面角的平面角,然后求解直角三角形得答案.
(1)分别取PD,PC的中点F,G,则FG∥CD∥AB,![]() ,
,
∴四边形AEGF为平行四边形,则AF∥EG,又FG平面PEC,
∴AF∥平面PEC,
∴PD的中点F即为所求;
(2)由PA⊥平面ABCD,可得平面PAB⊥平面ABCD,
∵E为AB中点,且BC=2BE=2,∠CBE=60°,∴CE⊥AB.
∴∠CPE即为PC与平面PAB所成的角,
在Rt△PEC中,![]() ,即
,即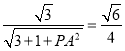 ,
,
解得:PA=2,
过D作BA的垂线,垂足为H,过H作PE的垂线,垂足为K,连接KD,
∵PA⊥平面ABCD,∴PA⊥DH,
又DH⊥BA,∴DH⊥平面PBA,
∴DH⊥PE,则PE⊥平面DHK,得PE⊥DH,
∴∠DKH即为所求的二面角的平面角,
在Rt△DHK中,![]() ,
,
由于PEHK=EHPA,∴![]() ,
,
从而![]() ,
,
∴![]() ,
,
即二面角D﹣PE﹣A的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
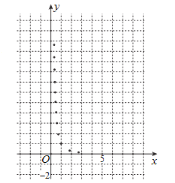
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关
关![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为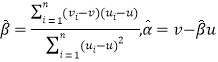 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() .如果数列
.如果数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“陪伴数列”.
的“陪伴数列”.
(Ⅰ)写出数列![]() 的“陪伴数列”
的“陪伴数列”![]() ;
;
(Ⅱ)若![]() 的“陪伴数列”是
的“陪伴数列”是![]() .试证明:
.试证明: ![]() 成等差数列.
成等差数列.
(Ⅲ)若![]() 为偶数,且
为偶数,且![]() 的“陪伴数列”是
的“陪伴数列”是![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交椭圆C于不同于N的A,B两点,直线NA,NB的斜率分别为k1,k2,问k1+k2是否为定值?若是的求出这个值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程是:
的方程是: ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设过原点的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别
的左右焦点分别![]()
![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点,满足
两点,满足![]() .
.
(1)求椭圆![]() 的离心率.
的离心率.
(2)![]() 是椭圆
是椭圆![]() 短轴的两个端点,设点
短轴的两个端点,设点![]() 是椭圆
是椭圆![]() 上一点(异于椭圆
上一点(异于椭圆![]() 的顶点),直线
的顶点),直线![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 的通项公式分别为
的通项公式分别为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]() (
(![]() ,
,![]() ),对任意
),对任意![]() ,
,![]() ,求出数列
,求出数列![]() 的最大项(用含
的最大项(用含![]() 式子表达).
式子表达).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com