
 }是等比数列.
}是等比数列. (Ⅱ)见解析
(Ⅱ)见解析 }是等比数列?
}是等比数列? 即可.
即可.
 首项,2为公比的等比数列,通项公式为
首项,2为公比的等比数列,通项公式为

 ,所以
,所以 ,
,
 }是以
}是以 为首项,公比为2的等比数列
为首项,公比为2的等比数列

科目:高中数学 来源:不详 题型:填空题
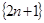 中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为
中各项划分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33), (35,37,39,41)。照此下去,第100个括号里各数的和为 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.8 | B.9 | C.10 | D.11 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 成等比数列,则
成等比数列,则 也成等比数列;②若数列{
也成等比数列;②若数列{ }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{ }为常数列;③数列{
}为常数列;③数列{ }的前n项和为
}的前n项和为 ,且
,且 ,则{
,则{ }为等差或等比数列;④数列{
}为等差或等比数列;④数列{ }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{ }中不会有
}中不会有 ,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______.(注:把你认为正确判断的序号都填上)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列 的首项和公比都为
的首项和公比都为 ,数列
,数列 和
和 的前
的前 项和分别为
项和分别为 ,且
,且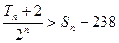 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com