
 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.

 的学生人数为
的学生人数为 (人),参加社区服务在时间段
(人),参加社区服务在时间段 的学生人数为
的学生人数为 (人).所以参加社区服务时间不少于90小时的学生人数为
(人).所以参加社区服务时间不少于90小时的学生人数为 (人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件
(人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件 .由(Ⅰ)可知,参加社区服务在时间段
.由(Ⅰ)可知,参加社区服务在时间段 的学生有4人,记为
的学生有4人,记为 ;参加社区服务在时间段
;参加社区服务在时间段 的学生有2人,记为
的学生有2人,记为 .从这6人中任意选取2人有
.从这6人中任意选取2人有 共15种情况.事件
共15种情况.事件 包括
包括 共7种情况.所以所选学生的服务时间在同一时间段内的概率
共7种情况.所以所选学生的服务时间在同一时间段内的概率 .
. 的学生人数为
的学生人数为 (人),
(人), 的学生人数为
的学生人数为 (人).
(人). (人). 5分
(人). 5分 .
. 的学生有4人,记为
的学生有4人,记为 ;
; 的学生有2人,记为
的学生有2人,记为 .
.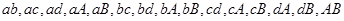 共15种情况.
共15种情况. 包括
包括 共7种情况.
共7种情况. . 13分
. 13分

 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com