
【题目】在△ABC中,已知AB=2,cosB= ![]() (Ⅰ)若AC=2
(Ⅰ)若AC=2 ![]() ,求sinC的值;
,求sinC的值;
(Ⅱ)若点D在边AC上,且AD=2DC,BD= ![]() ,求BC的长.
,求BC的长.
【答案】解:(Ⅰ)∵cosB= ![]() ,
,
∴sinB= ![]() =
= ![]() ,
,
∵ ![]() ,且AC=2
,且AC=2 ![]() ,AB=2,
,AB=2,
∴sinC= ![]() =
= ![]()
(Ⅱ)在△ABC中,设BC=a,AC=b,
∵AB=2,cosB= ![]() ,
,
∴由余弦定理可得:b2=a2+4﹣ ![]() ,①
,①
在△ABD和△BCD中,由余弦定理可得:
cos∠ADB= 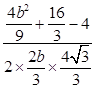 ,cos∠BDC=
,cos∠BDC= 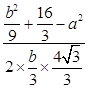 ,
,
∵cos∠ADB=﹣cos∠BDC,
∴ 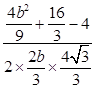 =﹣
=﹣ 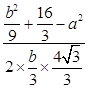 ,解得:
,解得: ![]() ﹣a2=﹣6,②
﹣a2=﹣6,②
∴由①②可得:a=3,b=3,即BC的值为3
【解析】(Ⅰ)由已知利用同角三角函数基本关系式可求sinB,利用正弦定理即可解得sinC的值.(Ⅱ)在△ABC中,设BC=a,AC=b,由余弦定理可得:b2=a2+4﹣ ![]() ,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得
,①,由于cos∠ADB=﹣cos∠BDC,利用余弦定理可得 ![]() ﹣a2=﹣6,②,联立即可得解BC的值.
﹣a2=﹣6,②,联立即可得解BC的值.


科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥ A1B1 , D为棱A1B1上的点.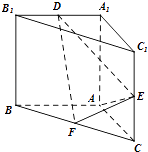
(1)证明:DF⊥AE;
(2)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2cos(x﹣ ![]() )的图象上所有的点的横坐标缩短到原来的
)的图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
A.关于点(﹣ ![]() ,0)对称
,0)对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABP7P5的边长为2,P1 , P4 , P6 , P2是四边的中点,AB是正方形的其中一条边,P1P6与P2P4相交于点P3 , 则 ![]()
![]() (i=1,2,…,7)的不同值的个数为( )
(i=1,2,…,7)的不同值的个数为( ) 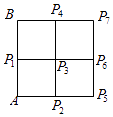
A.7
B.5
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图像中,与所给3件事吻合最好的顺序为( )
(1.)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2.)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3.)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.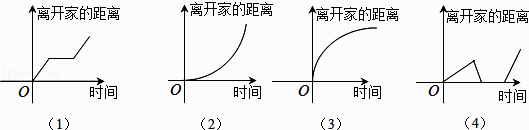
A.(4)(1)(2)
B.(4)(2)(3)
C.(4)(1)(3)
D.(1)(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 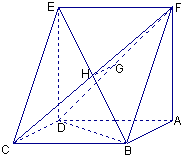
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com