
【题目】定义满足不等式|x![]() A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b
A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b![]() t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
科目:高中数学 来源: 题型:
【题目】某市小型机动车驾照“科二”考试中共有5项考察项目,分别记作①,②,③,④,⑤.
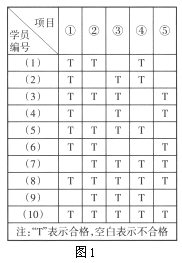
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如图1所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3项的概率;
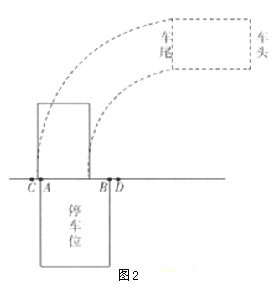
(2)如图2,某次模拟演练中,教练要求学员甲倒车并转向90°,在汽车边缘不压射线AC与射线BD的前提下,将汽车驶入指定的停车位. 根据经验,学员甲转向90°后可使车尾边缘完全落在线段CD,且位于CD内各处的机会相等.若CA="BD=0.3m," AB="2.4m." 汽车宽度为1.8m, 求学员甲能按教练要求完成任务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)确定![]() 的值;
的值;
(2)若![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() .
.
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 若存在![]() ,使不等式
,使不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)已知函数![]() 满足
满足![]() ,且规定
,且规定![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()

①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com