[题目]天气预报说.在今后的三天中.每一天下雨的概率均为.某同学用随机模拟的方法确定这三天中恰有两天下雨的概率.该同学利用计算器可以产生0到9之间的取整数值的随机数.他用1,4,7表示下雨.用0,2,3,5,6,8,9表示不下雨.实验得出如下20组随机数:245,368,590,126,217,895,560,061,378,902542,751,245,602,156 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】天气预报说，在今后的三天中，每一天下雨的概率均为，某同学用随机模拟的方法确定这三天中恰有两天下雨的概率，该同学利用计算器可以产生0到9之间的取整数值的随机数，他用1,4,7表示下雨，用0,2,3,5,6,8,9表示不下雨。实验得出如下20组随机数：

245,368,590,126,217,895,560,061,378,902

542,751,245,602,156,035,682,148,357,438

请根据该同学实验的数据确定这三天中恰有两天下雨的概率为 __________．

【答案】0.15

【解析】分析：由已知条件可知，20组随机数中有3组满足三天中恰有两天下雨，根据概率公式计算，即可得到答案.

详解：由题意可知，经随机模拟产生的20组随机数中，表示三天中恰有两天下雨的有：217，751，148.共3组随机数.

所求概率为.

故答案为.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知椭圆E的长轴的一个端点是抛物线的焦点，离心率是．

（1）求椭圆E的方程；

（2）过点，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使为常数？若存在，求出点M的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数是偶函数.

（1）求证：是偶函数；

（2）求证：在上是增函数；

（3）设（，且），若对任意的，在区间上总存在两个不同的数，，使得成立，求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为比较甲、乙两地某月14时的气温情况，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图，考虑以下结论：

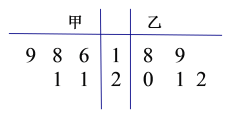
①甲地该月14时的平均气温低于乙地该月14时的平均气温；

②甲地该月14时的平均气温高于乙地该月14时的平均气温；

③甲地该月14时的平均气温的标准差小于乙地该月14时的平均气温的标准差；

④甲地该月14时的平均气温的标准差大于乙地该月14时的平均气温的标准差，

其中根据茎叶图能得到的统计结论的编号为（）

A. ①③ B. ①④ C. ②③ D. ②④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知各项为正数的数列{an}的前n项和为Sn ，且满足
（Ⅰ）求证：{an}为等差数列，并求数列{an}的通项公式；
（Ⅱ）设，求证：．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】微信是现代生活进行信息交流的重要工具，据统计，某公司名员工中的人使用微信，其中每天使用微信时间在一小时以内的有人，其余每天使用微信在一小时以上．若将员工年龄分成青年（年龄小于岁）和中年（年龄不小于岁）两个阶段，使用微信的人中是青年人．若规定：每天使用微信时间在一小时以上为经常使用微信，经常使用微信的员工中是青年人．