
【题目】某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
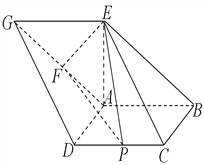
【题目】如图,已知四边形![]() 和
和![]() 均为平行四边形,点
均为平行四边形,点![]() 在平面
在平面![]() 内的射影恰好为点
内的射影恰好为点![]() ,以
,以![]() 为直径的圆经过点
为直径的圆经过点![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从![]() 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到
两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到![]() 地区用户满意度评分的频率分布直方图和
地区用户满意度评分的频率分布直方图和![]() 地区用户满意度评分的频数分布表.
地区用户满意度评分的频数分布表.
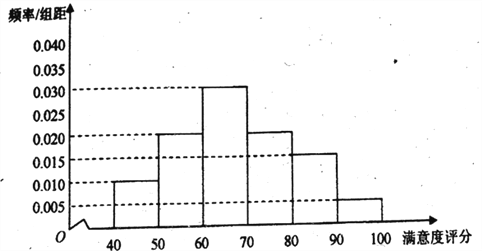
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
![]() 地区用户满意度评分的频数分布表
地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
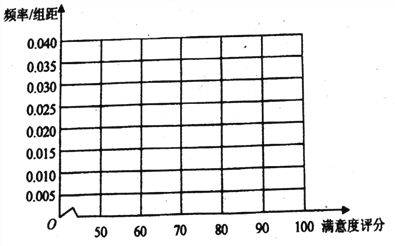
(1)在答题卡上作出![]() 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(2)根据用户满意度评分,将用户的满意度从低到高分为三个等级:

估计哪个地区的满意度等级为不满意的概率大?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归方程![]() =
=![]() x+
x+![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的粮食需求量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 是
是![]() 的必要而不充分条件;
的必要而不充分条件;
设命题![]() 实数
实数![]() 满足方程
满足方程![]() 表示双曲线.
表示双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 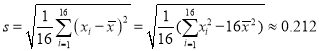 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如下:
,数学成绩的频率分布直方图如下:
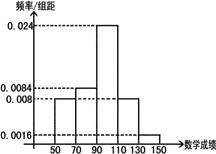
(Ⅰ)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布的)
(Ⅱ)如果语文和数学两科都特别优秀的共有6人,从(Ⅰ)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com