
【题目】某中学高三(3)班全班50人参加了高考前的数学模拟测试,每名学生要在规定的2个小时内做一套高三模拟卷,现抽取10位学生的成绩,分为甲,乙两组,其分数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 64 | 72 | 86 | 98 | 120 |
乙组 | 60 | 76 | 90 | 92 | 122 |
(Ⅰ)分别求出甲,乙两组学生考试所得分数的平均数及方差,并由此分析两组学生的成绩水平;
(Ⅱ)试估计全班有多少人及格(90分及以上为及格);
(Ⅲ)从该班级甲,乙两组中各随机抽取1名学生,对其考试成绩进行抽查,求两人考试分数之和大于等于180的概率.
【答案】(Ⅰ)88,88,392,420.8,两组学生的总体水平相同.甲组学生的成绩水平差异比乙组的小;(Ⅱ)25;(Ⅲ)![]() .
.
【解析】
(Ⅰ)根据平均数的计算公式,方差的计算公式,即可求出结果;
(Ⅱ)先由题意求出10位学生中及格的频率,进而可求出结果;
(Ⅲ)先设事件![]() 表示:从甲,乙两组中各抽取一名学生,两人考试分数之和大于等于180,用列举法,列出总的基本事件,以及事件
表示:从甲,乙两组中各抽取一名学生,两人考试分数之和大于等于180,用列举法,列出总的基本事件,以及事件![]() 包含的基本事件,基本事件个数比即为所求概率.
包含的基本事件,基本事件个数比即为所求概率.
(Ⅰ)依题中的数据可得:![]() 甲
甲![]() ,
,
![]() 乙
乙![]() .
.
![]()
![]()
![]()
![]() .
.
因为![]()
![]() ,
,![]() ,所以两组学生的总体水平相同.甲组学生的成绩水平差异比乙组的小.
,所以两组学生的总体水平相同.甲组学生的成绩水平差异比乙组的小.
(Ⅱ)根据表格可知,10位学生中及格的概率为![]() .
.
所以估计全班及格的人数为![]() .
.
(Ⅲ)设事件![]() 表示:从甲,乙两组中各抽取一名学生,两人考试分数之和大于等于180,则从甲,乙两组中各抽取1名学生.两人的考试成绩可组成的基本事件为
表示:从甲,乙两组中各抽取一名学生,两人考试分数之和大于等于180,则从甲,乙两组中各抽取1名学生.两人的考试成绩可组成的基本事件为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共25种;
,共25种;
事件![]() 包含的基本事件有
包含的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,共11种,
,共11种,
故由古典概型,得![]() ,即从甲、乙两组中各抽取一名学生,两人考试分数之和大于等于180的概率为
,即从甲、乙两组中各抽取一名学生,两人考试分数之和大于等于180的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】空气质量指数(简称:AQI)是定量描述空气质量状况的无量纲指数,空气质量按照AQI大小分为六级:![]() 为优,
为优,![]() 为良,
为良,![]() 为轻度污染,
为轻度污染,![]() 为中度污染,
为中度污染,![]() 为重度污染,
为重度污染,![]() 为严重污染.下面记录了北京市
为严重污染.下面记录了北京市![]() 天的空气质量指数,根据图表,下列结论错误的是( )
天的空气质量指数,根据图表,下列结论错误的是( )
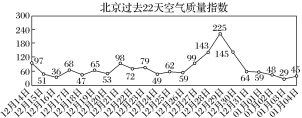
A.在北京这![]() 天的空气质量中,按平均数来考查,最后
天的空气质量中,按平均数来考查,最后![]() 天的空气质量优于最前面
天的空气质量优于最前面![]() 天的空气质量
天的空气质量
B.在北京这![]() 天的空气质量中,有
天的空气质量中,有![]() 天达到污染程度
天达到污染程度
C.在北京这![]() 天的空气质量中,
天的空气质量中,![]() 月
月![]() 日空气质量最差
日空气质量最差
D.在北京这![]() 天的空气质量中,达到空气质量优的天数有
天的空气质量中,达到空气质量优的天数有![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点O,其右焦点为F(1,0),以坐标原点O为圆心,椭圆短半轴长为半径的圆与直线x﹣y![]() 0的相切.
0的相切.
(1)求椭圆C的方程;
(2)经过点F的直线l1,l2分别交椭圆C于A、B及C、D四点,且l1⊥l2,探究:是否存在常数λ,使![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年新课标Ⅱ卷理综物理高考试题的选择题是这样的:二、选择题:本题共8小题,每小题6分,共48分,在每小题给出的四个选项中,第14~18题只有一项符合题目要求.第19~21题有多项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分,每年高考后都会对每题的得分情况进行一个大致的统计,特地对第19题的得分情况进调研,从某省所有试卷中随机抽取1000份试卷,其中第19题的得分组成容量为1000的样本.统计结果如下表:
得分 | 0 | 3 | 6 |
人数 | 200 | 300 | 500 |
(1)求这1000份试卷中第19题的得分的中位数和平均数;
(2)若某校的两名高三学生因故未参加考试,如果这两名学生参加考试,以样本中各种得分情况的频率作为这两名同学相应的各种得分情况的概率.试求这两名同学理综卷第19题的得分之和![]() 的分布列及效学期望.
的分布列及效学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有曲池,上中周二丈,外周四丈,广一丈,下中周一丈四尺,外周二丈四尺,广五尺,深一丈,问积几何?”其意思为:“今有上下底面皆为扇形的水池,上底中周2丈,外周4丈,宽1丈;下底中周1丈4尺,外周长2丈4尺,宽5尺;深1丈.问它的容积是多少?”则该曲池的容积为( )立方尺(1丈=10尺,曲池:上下底面皆为扇形的土池,其容积公式为![]() [(2×上宽+下宽)
[(2×上宽+下宽)![]() (2×下宽+上宽)
(2×下宽+上宽)![]() ]×深)
]×深)
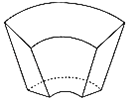
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,
,![]() 在该抛物线上且位于
在该抛物线上且位于![]() 轴的两侧,
轴的两侧,![]() .
.
(Ⅰ)证明:直线![]() 过定点
过定点![]() ;
;
(Ⅱ)以![]() ,
,![]() 为切点作
为切点作![]() 的切线,设两切线的交点为
的切线,设两切线的交点为![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com