练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】旅游社为某旅游团包飞机去旅游，其中旅行社的包机费为15 000元．旅游团中每人的飞机票按以下方式与旅行社结算：若旅游团人数在30人或30人以下，飞机票每张收费900元；若旅游团人数多于30人，则给予优惠，每多1人，机票费每张减少10元，但旅游团人数最多为75人．

    (1)写出飞机票的价格关于旅游团人数的函数；

    (2)旅游团人数为多少时，旅行社可获得最大利润？

    【答案】（1）.

    (2) 旅游团人数为60时，旅行社可获得最大利润．

    【解析】

    （1）根据自变量 的取值范围，分0或，确定每张飞机票价的函数关系式；
    （Ⅱ）利用所有人的费用减去包机费就是旅行社可获得的利润，结合自变量的取值范围，可得利润函数，结合自变量的取值范围，分段求出最大利润，从而解决问题．

    (1)设旅游团人数为人，飞行票价格为元，依题意，当，且时，，当，且时，y＝900－10(x－30)＝－10x＋1 200.

    所以所求函数为

    y＝

    (2)设利润为元，则

    当，且时， (元)，

    当，且时，元，因为21 000元>12 000元，

    所以旅游团人数为60时，旅行社可获得最大利润．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列各组中的两个集合相等的有(　　)

    ①P＝{x|x＝2n，n∈Z}，Q＝{x|x＝2(n－1)，n∈Z}；

    ②P＝{x|x＝2n－1，n∈N*}，Q＝{x|x＝2n＋1，n∈N*}；

    ③P＝{x|x2－x＝0}，Q＝.

    A. ①②③ B. ①③

    C. ②③ D. ①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax2﹣blnx在点（1，f（1））处的切线为y=1．
    （Ⅰ）求实数a，b的值；
    （Ⅱ）是否存在实数m，当x∈（0，1]时，函数g（x）=f（x）﹣x2+m（x﹣1）的最小值为0，若存在，求出m的取值范围；若不存在，说明理由；
    （Ⅲ）若0＜x1＜x2 ， 求证： ＜2x2 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图：设一正方形纸片ABCD边长为2分米，切去阴影部分所示的四个全等的等腰三角形，剩余为一个正方形和四个全等的等腰三角形，沿虚线折起，恰好能做成一个正四棱锥（粘接损耗不计），图中，O为正四棱锥底面中心．

    （Ⅰ）若正四棱锥的棱长都相等，求这个正四棱锥的体积Ｖ；

    （Ⅱ）设等腰三角形APQ的底角为x，试把正四棱锥的侧面积S表示为x的函数，并求S的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学在用120分钟做150分的数学试卷(分为卷Ⅰ和卷Ⅱ两部分)时，卷Ⅰ和卷Ⅱ所得分数分别为P(单位：分)和Q(单位：分)，在每部分做了20分钟的条件下发现它们与投入时间m(单位：分钟)的关系有经验公式，.

    (1)试建立数学总成绩y(单位：分)与对卷Ⅱ投入时间x(单位：分钟)的函数关系式，并指明函数定义域；

    (2)如何计划使用时间，才能使得所得分数最高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，且．

    (1)判断函数的奇偶性；

    (2) 判断函数在(1，＋∞)上的单调性，并用定义证明你的结论；

    (3)若，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知矩形的长为2，宽为1， ， 边分别在轴、轴的正半轴上， 点与坐标原点重合，将矩形折叠，使点落在线段上，设此点为.

    （1）若折痕的斜率为-1，求折痕所在的直线的方程；

    （2）若折痕所在直线的斜率为，（ 为常数），试用表示点的坐标，并求折痕所在的直线的方程；

    （3）当时，求折痕长的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，经过点且斜率为的直线与椭圆有两个不同的交点和．

    （1）求的取值范围；

    （2）设椭圆与轴正半轴、轴正半轴的交点分别为，是否存在常数，使得向量与共线？如果存在，求值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

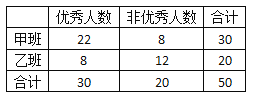
    【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关，某校兴趣小组为了验证这个结论，从该校选择甲乙两个同轨班级进行试验，其中甲班加强阅读理解训练，乙班常规教学无额外训练，一段时间后进行数学应用题测试，统计数据情况如下面的列联表（单位：人）

    （1）经过多次测试后，小明正确解答一道数学应用题所用的时

    间在5—7分钟，小刚正确解得一道数学应用题所用的时间在6—8

    分钟，现小明.小刚同时独立解答同一道数学应用题，求小刚比

    小明先正确解答完的概率；

    （2）现从乙班成绩优秀的8名同学中任意抽取两人，并对他们的答题情况进行全程研究，记A.B两人中被抽到的人数为，求的分布列及数学期望.

    查看答案和解析>>

    同步练习册答案