已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y)又当 x2>x1>0时,f(x2)>f(x1)
(1)求f(1),f(4),f(8)的值;
(2)若有f(2x-5)≤3成立,求x的取值范围.
【答案】
分析:(1)由f(xy)=f(x)+f(y),通过赋值法即可求得f(1),f(4),f(8)的值;
(2)由“x
2>x
1>0时,f(x
2)>f(x
1)”可知f(x)在定义域(0,+∞)上为增函数,从而f(2x-5)≤3=f(8)可脱去函数“外衣”,求得x的取值范围.
解答:解:(1)由f(xy)=f(x)+f(y)得:f(1•1)=f(1)+f(1)⇒f(1)=0;…2分
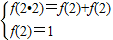
⇒f(4)=2;…2分
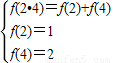
⇒f(8)=3;…2分
(2)由“x
2>x
1>0时,f(x
2)>f(x
1)”得f(x)在定义域(0,+∞)上为增函数;…2分
∴
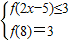
⇒f(2x-5)≤f(8)⇒
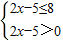
⇒

<x≤
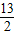
…2分
点评:本题考查抽象函数及其应用,考查函数单调性的性质及函数求值,(2)中判断函数f(x)在定义域(0,+∞)上为增函数是关键,属于中档题.

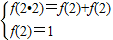 ⇒f(4)=2;…2分
⇒f(4)=2;…2分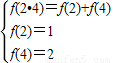 ⇒f(8)=3;…2分
⇒f(8)=3;…2分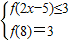 ⇒f(2x-5)≤f(8)⇒
⇒f(2x-5)≤f(8)⇒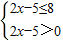 ⇒
⇒ <x≤
<x≤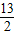 …2分
…2分

 阅读快车系列答案
阅读快车系列答案