练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设 是两个平面， 是两条直线，有下列四个命题：
    ⑴如果 ，那么 .
    ⑵如果 ，那么 .
    ⑶如果 ，那么 .
    其中正确命题的个数是（ ）
    A.0
    B.1
    C.2
    D.3

    【答案】C
    【解析】对于①， ，则 的位置关系无法确定，故错误；对于②,因为 ，所以过直线 作平面 与平面 相交于直线 ，则 c，因为 , , ，故②正确；对于③，由两个平面平行的性质可知正确；所以答案是：


    【考点精析】掌握直线与平面平行的判定和直线与平面平行的性质是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

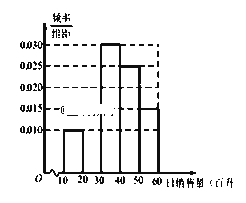
    【题目】某加油站20名员工日销售量的频率分布直方图，如图所示：

    （1）补全该频率分布直方图在[20，30）的部分，并分别计算日销售量在 [10，20），[20，30）的员工数；

    （2）在日销量为[10，30）的员工中随机抽取2人，求这两名员工日销量在 [20，30）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （I）求函数 在点 处的切线方程；
    （II）求函数 的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】研究函数f（x）= 的性质，完成下面两个问题：
    ①将f（2），f（3），f（5）按从小到大排列为；
    ②函数g（x）= （x> 0）的最大值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，AA1⊥底面ABCD，E为B1D的中点．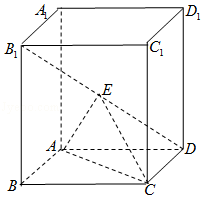
    （Ⅰ）证明：平面ACE⊥平面ABCD；
    （Ⅱ）若二面角D﹣AE﹣C为60°，AA1=AB=1，求三棱锥C﹣AED的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

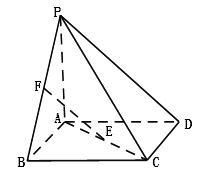
    【题目】如图，四棱锥 的底面 为正方形， ⊥底面 ， 分别是 的中点， .

    （Ⅰ）求证 ∥平面 ；
    （Ⅱ）求直线 与平面 所成的角；
    （Ⅲ）求四棱锥 的外接球的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体中， 菱形， 是矩形， ⊥平面 ， ， .

    （Ⅰ）异面直线 与 所成的角余弦值；
    （Ⅱ）求证平面 ⊥平面 ；
    （Ⅲ）在线段 取一点 ，当二面角 的大小为60°时，求 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某化工厂拟建一个下部为圆柱，上部为半球的容器（如图圆柱高为 ，半径为 ，不计厚度，单位：米），按计划容积为 立方米，且 ，假设建造费用仅与表面积有关（圆柱底部不计 ），已知圆柱部分每平方米的费用为2千元，半球部分每平方米的费用为2千元，设该容器的建造费用为y千元.

    （1）求y关于r的函数关系，并求其定义域；
    （2）求建造费用最小时的 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片，按下列规则，把金属片从一根针上全部移到另一根针上：①每次只能移动一个金属片；②在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面．将n个金属片从1号针移到3号针最少需要移动的次数记为f（n），则f（6）=（ ）
    A.31
    B.33
    C.63
    D.65

    查看答案和解析>>

    同步练习册答案