
| 2sin2α-3cos2α | 4sin2α-9cos2α |
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:江西省新余一中2010届高三第六次模拟考试数学理科试题 题型:044
已知sin(2α+β)=3sinβ,设tanα=x,tanβ=y,记y=f(x).
(1)求f(x)的表达式;
(2)定义正数数列{an}:a1=![]() ,
,![]() =2an·f(an)(n∈N*).试求数列{an}的通项公式;
=2an·f(an)(n∈N*).试求数列{an}的通项公式;
(3)在(2)的条件下,记bn= ,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知双曲线![]() (a>0,b>0)的上、下顶点分别为A、B,一
(a>0,b>0)的上、下顶点分别为A、B,一
个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列.
(1)求双曲线的方程;
(2)设过点F作直线l交双曲线上支于M、N两点,如果S△MON=![]() tan∠MON,求△MBN的面积.
tan∠MON,求△MBN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知双曲线![]() (a>0,b>0)的上、下顶点分别为A、B,一
(a>0,b>0)的上、下顶点分别为A、B,一
个焦点为F(0,c)(c>0),两准线间的距离为1,|AF|、|AB|、|BF|成等差数列.
(1)求双曲线的方程;
(2)设过点F作直线l交双曲线上支于M、N两点,如果S△MON=![]() tan∠MON,求△MBN的面积.
tan∠MON,求△MBN的面积.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省南通市如皋市、海安县高一(上)期末数学试卷(解析版) 题型:解答题
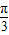 )(x∈R),且
)(x∈R),且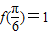 .
.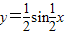 的图象;
的图象;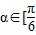 ,
,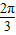 ,
,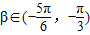 ,
,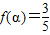 ,f(β)=-
,f(β)=- ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com