求经过两条直线l1:3x+4y-2=0与l2:2x+y+2=0的交点P,且垂直于直线l3:x-2y-1=0直线l的方程.
【答案】
分析:联立两个直线解析式先求出l
1和l
2的交点坐标,然后利用直线与直线l
3垂直,根据斜率乘积为-1得到直线l的斜率,写出直线l方程即可.
解答:解:解方程组
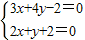
,得交点(-2,2).
又由l⊥l
3,且k
3=

,
因为两直线垂直得斜率乘积为-1,
得到k
l=-2,
∴直线l的方程为y-2=-2(x+2),即2x+y+2=0.
点评:考查学生求两条直线交点坐标的方法,会利用两直线垂直时斜率乘积等于-1解题的能力,会根据一个点和斜率写出直线一般式方程.属于基础题.
