
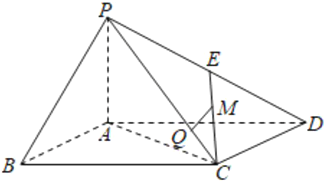
【题目】如图,在四棱锥P-ABCD中,![]()
![]()
![]()
![]() ,
,![]() 平面PAB,
平面PAB,![]() ,点E满足
,点E满足![]() .
.
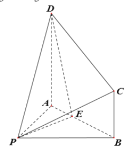
(1)证明:![]() ;
;
(2)求二面角A-PD-E的余弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)由勾股定理计算出![]() ,然后求数量积
,然后求数量积![]() 得
得![]() ,由线面垂直可得
,由线面垂直可得![]() ,从而可证得
,从而可证得![]() 平面ABCD得证线线垂直;
平面ABCD得证线线垂直;
(2)建立如图所示的直角坐标系,用空间向量法求二面角的余弦值.
(1)证明:在![]() 中,
中,
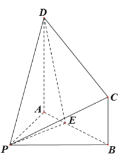
由勾股定理,得
![]()
![]()
![]() .
.
因为![]()
![]() ,
,
所以![]()
![]()
![]()
![]() .
.
所以![]() ,所以
,所以![]() .
.
因为![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
所以![]() .
.
又因为![]()
![]() ,
,
所以![]() 平面ABCD.
平面ABCD.
又因为![]() 平面ABCD,
平面ABCD,
所以![]() .
.
(2)由![]() 得
得![]() .
.
所以点E是靠近点A的线段AB的三等分点.
所以![]() .
.
分别以![]()
![]() 所在方向为y轴,z轴的正方向,建立如图所示的空间直角坐标系
所在方向为y轴,z轴的正方向,建立如图所示的空间直角坐标系![]() .
.
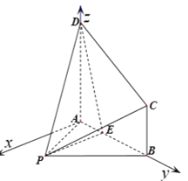
则![]()
![]()
![]()
![]() .
.
设平面PDE的法向量为![]() ,
,
由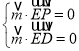 ,得
,得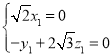 .
.
令![]() ,则
,则![]() ;
;
设平面APD的法向量为![]()
![]()
![]() ,
,
由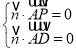 ,得
,得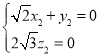 ,
,
令![]() ,则
,则![]() .
.
设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
则![]()
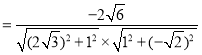
![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上且
上且![]() .
.
(1)证明![]() 平面
平面![]() ;
;
(2)当![]() 为多大时,在线段
为多大时,在线段![]() 上存在点
上存在点![]() 使得
使得![]() 平面
平面![]() 且
且![]() 与平面
与平面![]() 所成角为
所成角为![]() 同时成立?
同时成立?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式。孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P是圆F1:(x+1)2+y2=16上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)记曲线C与x轴交于A,B两点,M是直线x=1上任意一点,直线MA,MB与曲线C的另一个交点分别为D,E,求证:直线DE过定点H(4,0).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com