
【题目】四面体P﹣ABC中,PA![]() ,PB=PC=AB=AC=2,BC=2
,PB=PC=AB=AC=2,BC=2![]() ,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足
,动点Q在△ABC的内部(含边界),设∠PAQ=α,二面角P﹣BC﹣A的平面角的大小为β,△APQ和△BCQ的面积分别为S1和S2,且满足![]() ,则S2的最大值为_____.
,则S2的最大值为_____.
【答案】4﹣2![]() .
.
【解析】
取BC的中点M,由题意可得AM=PM=PA![]() ,则β=∠PMA=60°,作QH⊥BC于H,则
,则β=∠PMA=60°,作QH⊥BC于H,则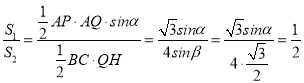 sinα,再由BC=2PA=2
sinα,再由BC=2PA=2![]() ,可得AQ=QH,即Q为三角形ABC内的一条抛物线,当Q在AB或AC上时,S2最大,求出S2的最大值.
,可得AQ=QH,即Q为三角形ABC内的一条抛物线,当Q在AB或AC上时,S2最大,求出S2的最大值.
如图所示:
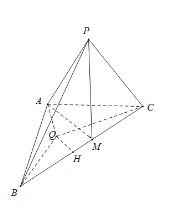
取BC的中点M,连接AM,PM,
因为PB=PC=AB=AC,
AM⊥BC,PM⊥BC,且PA![]() ,PB=PC=AB=AC=2,BC=2
,PB=PC=AB=AC=2,BC=2![]() ,
,
所以AM=PM=PA![]() ,
,
所以β=∠PMA=60°,
作QH⊥BC于H,
所以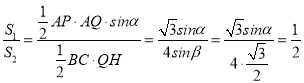 sinα,
sinα,
所以![]()
而BC=2PA=2![]() ,
,
所以AQ=QH,
所以Q的轨迹是△ABC内的一条抛物线,
当Q在AB或AC上时,S2最大,
不妨设在AB上,此时![]() ,
,
即![]() ,
,
解得AQ=QH=2(![]() 1),
1),
所以S2=4﹣2![]() .
.
故答案为:4﹣2![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
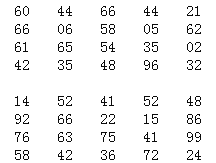
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2是椭圆C:![]() (a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为
(a>b>0)的左、右焦点,过椭圆的上顶点的直线x+y=1被椭圆截得的弦的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F1的直线l交椭圆于A,B两点,当△ABF2面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.①若定点为![]() ,写出
,写出![]() 的一个阿波罗尼斯圆的标准方程__________;②△
的一个阿波罗尼斯圆的标准方程__________;②△![]() 中,
中,![]() ,则当△
,则当△![]() 面积的最大值为
面积的最大值为![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为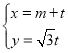 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和C的直角坐标方程;
的普通方程和C的直角坐标方程;
(2)直线![]() 上的点
上的点![]() 为曲线
为曲线![]() 内的点,且直线
内的点,且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直四棱柱![]() 中,底面
中,底面![]() 是边长为6的正方形,点
是边长为6的正方形,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,过点
,过点![]() 作直四棱柱
作直四棱柱![]() 外接球的截面,所得的截面面积的最大值与最小值之差为
外接球的截面,所得的截面面积的最大值与最小值之差为![]() ,则直四棱柱
,则直四棱柱![]() 外接球的半径为( )
外接球的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
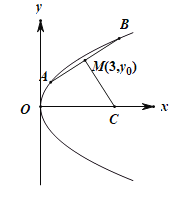
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招聘员工,指定三门考试课程,有两种考试方案.方案一:考试三门课程,至少有两门及格为考试通过;方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.假设某应聘者对三门指定课程考试及格的概率分别是![]() ,
,![]() ,
,![]() ,且三门课程考试是否及格相互之间没有影响.
,且三门课程考试是否及格相互之间没有影响.
(1)分别求该应聘者用方案一和方案二时考试通过的概率;
(2)试比较该应聘者在上述两种方案下考试通过的概率的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com