
| 2 | 3 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| 64 |
| 81 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
| 64 |
| 81 |
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 81 |
| X | 3 | 4 | 5 |
| P(X) | P3+P3′ | P4+P4′ | P5+P5′ |
| 1 |
| 27 |
| 8 |
| 27 |
| 8 |
| 27 |
| 2 |
| 27 |
| 16 |
| 81 |
| 8 |
| 81 |
| 107 |
| 27 |


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为![]() .
.
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设甲比赛的次数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源:2013届北京市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,决出胜负即停止比赛。按以往的比赛经验,每局比赛中,甲胜乙的概率为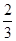 。
。
(1)求比赛三局甲获胜的概率;
(2)求甲获胜的概率;
(3)设比赛的局数为X,求X的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com