
【题目】已知函数f(x)= ![]() .(x>0)
.(x>0)
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)若当x>0时,f(x)> ![]() 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
【答案】
(1)解:函数f(x)= ![]()
∴f′(x)= ![]() [
[ ![]() ﹣1﹣ln(x+1)]=﹣
﹣1﹣ln(x+1)]=﹣ ![]() [
[ ![]() +ln(x+1)].
+ln(x+1)].
由x>0,x2>0, ![]() >0,ln(x+1)>0,得f′(x)<0.
>0,ln(x+1)>0,得f′(x)<0.
因此函数f(x)在区间(0,+∞)上是减函数
(2)解:解法一:当x>0时,f(x)> ![]() 恒成立,令x=1有k<2[1+ln2].
恒成立,令x=1有k<2[1+ln2].
又k为正整数.则k的最大值不大于3.
下面证明当k=3时,f(x)> ![]() (x>0)恒成立.
(x>0)恒成立.
即证明x>0时(x+1)ln(x+1)+1﹣2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1﹣2x,
则g′(x)=ln(x+1)﹣1.
当x>e﹣1时,g′(x)>0;当0<x<e﹣1时,g′(x)<0.
∴当x=e﹣1时,g(x)取得最小值g(e﹣1)=3﹣e>0.
∴当x>0时,(x+1)ln(x+1)+1﹣2x>0恒成立.
因此正整数k的最大值为3.
解法二:当x>0时,f(x)> ![]() 恒成立.
恒成立.
即h(x)= ![]() >k对x>0恒成立.
>k对x>0恒成立.
即h(x)(x>0)的最小值大于k.
由h′(x)= ![]() ,记Φ(x)=x﹣1﹣ln(x+1).(x>0)
,记Φ(x)=x﹣1﹣ln(x+1).(x>0)
则Φ′(x)= ![]() >0,
>0,
∴Φ(x)在(0,+∞)上连续递增.
又Φ(2)=1﹣ln3<0,Φ(3)=2﹣2ln2>0,
∴Φ(x)=0存在惟一实根a,且满足:a∈(2,3),a=1+ln(a+1),
由x>a时,Φ(x)>0,h′(x)>0;0<x<a时,Φ(x)<0,h′(x)<0知:
h(x)(x>0)的最小值为h(a)= ![]() =a+1∈(3,4).
=a+1∈(3,4).
因此正整数k的最大值为3
【解析】(1)直接求函数f(x)的导函数,化简导函数分子,判断正负即可;(2)可以先利用特殊值x=1先尝试k的可能值,然后用导数的方法予以证明;或者构造新函数将问题转化为求函数最值,利用函数的导数去研究函数的最值即可.


科目:高中数学 来源: 题型:
【题目】某校为了了解学生对周末家庭作业量的态度,拟采用分层抽样的方法分别从高一、高二、高三的高中生中随机抽取一个容量为200的样本进行调查,已知从700名高一、高二学生中共抽取了140名学生,那么该校有高三学生名.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosωx(sinωx+ ![]() cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
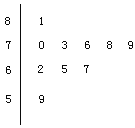
【题目】已知某单位有50名职工,现要从中抽取 10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组,按各组内抽取的编号依次增加5进行系统抽样.
(Ⅰ)若第5组抽出的号码为22,写出所有被抽出职工的号码;
(Ⅱ)分别统计这10名职工的体重(单位:公斤),获得体重数据的茎叶图如图所示,求该样本的平均数、中位数和方差;
(Ⅲ)在(Ⅱ)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤(![]() 73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
73公斤)的职工,求体重为81公斤的职工被抽取到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为f1(x)=2x﹣1,f2(x)=x3 , f3(x)=x,f4(x)=log2(x+1),有以下结论:
①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0<x<1时,丁走在最前面,当x>1时,丁走在最前面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 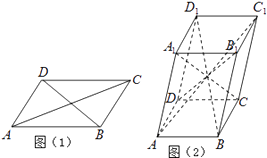
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图表示某人的体重与年龄的关系,则( )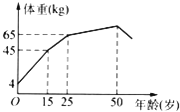
A.体重随年龄的增长而增加
B.25岁之后体重不变
C.体重增加最快的是15岁至25岁
D.体重增加最快的是15岁之前
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017桂林,百色,梧州,北海,崇左五市联合模考】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
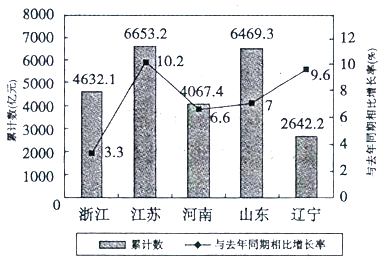
①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com