练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    给出下列命题：
    ①若平面α上的直线a与平面β上的直线b互为异面直线，c是α与β的交线，那么c至多与a、b中的一条相交；
    ②若直线a与b异面，过不在直线a、b上一点A可作一条与a和b都相交的直线；
    ③若直线a与b异面，则存在唯一 一个过a的平面α与b平行．
    其中正确的命题为（ ）
    A．①
    B．②
    C．③
    D．①③
    【答案】分析：画出图形判断①的正误；通过反例判断②的正误；利用直线与平面平行关系判断③的正误．
    解答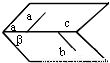：解：对于①，平面α上的直线a与平面β上的直线b互为异面直线，如图，c是α与β的交线，那么c至多与a、b中的一条相交；c与a、b都相交；故命题①不正确；
    对于②，若直线a与b异面，过不在直线a、b上一点A可作一条与a和b都相交的直线，例如正方体中，上下底面的异面直线，在上底面取步骤异面直线上的点，不存在满足②的直线．所以②不正确．
    对于③，假设过直线a有两个平面α、β与直线b平行，则面α、β相交于直线a，过直线b做一平面γ与面α、β相交于两条直线m、n，则直线m、n相交于一点，且都与直线b平行，这与“过直线外一点有且只有一条直线与已知直线平行”矛盾，所以假设不成立，所以③正确．
    故选C．
    点评：本题考查空间直线与直线、直线与平面的位置关系的判断，异面直线的应用，考查逻辑推理能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出下列命题：
    ①|
    a
    -
    b
    |≤|
    a
    |-|
    b
    |；②
    a
    ，
    b
    共线，
    b
    ，
    c
    平，则
    a
    与
    c
    为平行向量；③
    a
    ，
    b
    ，
    c
    为相互不平行向量，则（
    b
    -
    c
    ）
    a
    -（
    c
    -
    a
    ）
    b
    与
    c
    垂直；④在△ABC中，若a2taanB=b2tanA，则△ABC一定是等腰直角三角形；⑤
    a
    •
    b
    =
    a
    •
    c
    ，则
    a
    ⊥（
    b
    -
    c
    ）   
    其中错误的有
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设α、β、γ为彼此不重合的三个平面，l为直线，给出下列命题：
    ①若α∥β，α⊥γ，则β⊥γ，
    ②若α⊥γ，β⊥γ，且αnβ=l，则l⊥γ
    ③若直线l与平面α内的无数条直线垂直则直线l与平而α垂直，
    ④若α内存在不共线的三点到β的距离相等．则平面α平行于平面β
    上面命题中，真命题的序号为
    ①②
    ①②
    ．（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    给出下列命题：
    ①|
    a
    -
    b
    |≤|
    a
    |-|
    b
    |；②
    a
    ，
    b
    共线，
    b
    ，
    c
    平，则
    a
    与
    c
    为平行向量；③
    a
    ，
    b
    ，
    c
    为相互不平行向量，则（
    b
    -
    c
    ）
    a
    -（
    c
    -
    a
    ）
    b
    与
    c
    垂直；④在△ABC中，若a2taanB=b2tanA，则△ABC一定是等腰直角三角形；⑤
    a
    •
    b
    =
    a
    •
    c
    ，则
    a
    ⊥（
    b
    -
    c
    ）   
    其中错误的有______．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年河北省衡水中学高一（下）一调数学试卷（理科）（解析版） 题型：填空题

    给出下列命题：
    ①|-|≤||-||；②，共线，，平，则与为平行向量；③，，为相互不平行向量，则（）-（-）与垂直；④在△ABC中，若a2taanB=b2tanA，则△ABC一定是等腰直角三角形；⑤•=•，则⊥（-）   
    其中错误的有    ．

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省深圳市宝安中学高考数学考前热身训练试卷（文科）（解析版） 题型：解答题

    设α、β、γ为彼此不重合的三个平面，l为直线，给出下列命题：
    ①若α∥β，α⊥γ，则β⊥γ，
    ②若α⊥γ，β⊥γ，且αnβ=l，则l⊥γ
    ③若直线l与平面α内的无数条直线垂直则直线l与平而α垂直，
    ④若α内存在不共线的三点到β的距离相等．则平面α平行于平面β
    上面命题中，真命题的序号为    ．（写出所有真命题的序号）

    查看答案和解析>>

    同步练习册答案