
| AЃЎ | ЃЈ0ЃЌ$\frac{1}{3}$ЃЉ | BЃЎ | [$\frac{1}{3}$ЃЌ$\frac{1}{e}$ЃЉ | CЃЎ | ЃЈ$\frac{1}{e}$ЃЌ$\frac{4}{3}$] | DЃЎ | ЃЈ-ЁоЃЌ0]ЁШ[$\frac{4}{3}$ЃЌ+ЁоЃЉ |
ЗжЮі гЩЬтвтЃЌЗНГЬfЃЈxЃЉ=axЧЁгаСНИіВЛЭЌЪЕЪ§ИљЃЌЕШМлгкy=fЃЈxЃЉгыy=axга2ИіНЛЕуЃЌгжaБэЪОжБЯпy=axЕФаБТЪЃЌЧѓГіaЕФШЁжЕЗЖЮЇЃЎ
НтД№ НтЃКЁпЗНГЬfЃЈxЃЉ-ax=0ЧЁгаСНИіВЛЭЌЪЕЪ§ИљЃЌ
Ёрy=fЃЈxЃЉгыy=axга2ИіНЛЕуЃЌ
гжЁпaБэЪОжБЯпy=axЕФаБТЪЃЌ
ЁрxЃО1ЪБЃЌyЁф=$\frac{1}{x}$ЃЌ
ЩшЧаЕуЮЊЃЈx0ЃЌy0ЃЉЃЌk=$\frac{1}{{x}_{0}}$ЃЌ
ЁрЧаЯпЗНГЬЮЊy-y0=$\frac{1}{{x}_{0}}$ЃЈx-x0ЃЉЃЌ
ЖјЧаЯпЙ§дЕуЃЌЁрy0=1ЃЌx0=eЃЌk=$\frac{1}{e}$ЃЌ
ЁржБЯпl1ЕФаБТЪЮЊ$\frac{1}{e}$ЃЌ
гжЁпжБЯпl2гыy=$\frac{1}{3}$x+1ЦНааЃЌ
ЁржБЯпl2ЕФаБТЪЮЊ$\frac{1}{3}$ЃЌ
ЁрЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ[$\frac{1}{3}$ЃЌ$\frac{1}{e}$ЃЉ
ЙЪбЁЃКBЃЎ
ЕуЦР БОЬтПМВщСЫКЏЪ§ЕФЭМЯѓгыаджЪЕФгІгУЮЪЬтЃЌПМВщКЏЪ§гыЗНГЬЕФЙиЯЕЃЌЪЧвзДэЬтЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{\sqrt{7}}{4}$ | BЃЎ | $\frac{\sqrt{7}}{3}$ | CЃЎ | $\frac{1}{4}$ | DЃЎ | $\frac{4}{5}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | fЃЈxЃЉ=|2x-1| | BЃЎ | fЃЈxЃЉ=ex | CЃЎ | fЃЈxЃЉ=x2+x+1 | DЃЎ | fЃЈxЃЉ=sinx |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{1}{5}$ | BЃЎ | -$\frac{1}{5}$ | CЃЎ | $\frac{7}{5}$ | DЃЎ | -$\frac{7}{5}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
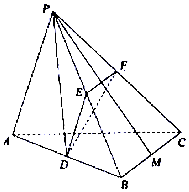 ШчЭМЃЌвбжЊШ§РтзЖP-ABCЃЌBCЁЭACЃЌBC=AC=2ЃЌPA=PBЃЌЦНУцPABЁЭЦНУцABCЃЌDЁЂEЁЂFЗжБ№ЪЧABЁЂPBЁЂPCЕФжаЕуЃЎ
ШчЭМЃЌвбжЊШ§РтзЖP-ABCЃЌBCЁЭACЃЌBC=AC=2ЃЌPA=PBЃЌЦНУцPABЁЭЦНУцABCЃЌDЁЂEЁЂFЗжБ№ЪЧABЁЂPBЁЂPCЕФжаЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ШчЙћl1ЁЮІСЃЌl2ЁЮІСЃЌдђвЛЖЈгаl1ЁЮl2 | BЃЎ | ШчЙћl1ЁЭl2ЃЌl2ЁЭІСЃЌдђвЛЖЈгаl1ЁЭІС | ||
| CЃЎ | ШчЙћl1ЁЭl2ЃЌl2ЁЭІСЃЌдђвЛЖЈгаl1ЁЮІС | DЃЎ | ШчЙћl1ЁЭІСЃЌl2ЁЮІСЃЌдђвЛЖЈгаl1ЁЭl2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2+$\sqrt{3}$ | BЃЎ | 5+2$\sqrt{6}$ | CЃЎ | 8+$\sqrt{15}$ | DЃЎ | 2$\sqrt{3}$ |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com