练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

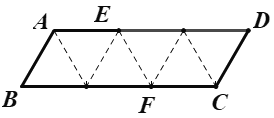
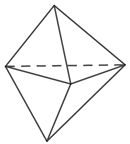
    【题目】如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的表面积为__________；若该六面体内有一小球，则小球的最大体积为___________．

    【答案】

    【解析】

    （1）计算每个面的面积再乘以6，即可得到答案；

    （2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时，求出球的半径，再代入球的体积公式可得答案.

    （1）因为，所以该六面体的表面积为.

    （2）由图形的对称性得，小球的体积要达到最大，即球与六个面都相切时，

    每个三角形面积是，六面体体积是正四面体的2倍，所以六面体体积是.

    由于图像的对称性，内部的小球要是体积最大，就是球要和六个面相切，连接球心和五个顶点，把六面体分成了六个三棱锥，设球的半径为，

    所以，

    所以球的体积.

    故答案为： ；.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 ， ,

    ⑴ 若有零点，求 m 的取值范围；

    ⑵ 确定 m 的取值范围，使得有两个相异实根.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数,当时,恒成立,则的最大值是_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

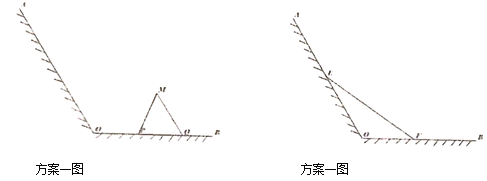
    【题目】江心洲有一块如图所示的江边，，为岸边，岸边形成角，现拟在此江边用围网建一个江水养殖场，有两个方案：方案l：在岸边上取两点，用长度为的围网依托岸边线围成三角形（，两边为围网）；方案2：在岸边，上分别取点，用长度为的围网依托岸边围成三角形.请分别计算，面积的最大值，并比较哪个方案好.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数f（x）＝｜x﹣m｜+｜x｜，m∈N*，存在实数x使f（x）＜2成立．

    （1）求实数m的值；

    （2）若α≥1，β≥1，f（α）+f（β）＝4，求证：≥3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在坐标原点，焦点在轴上，左顶点为，左焦点为，点在椭圆上，直线与椭圆交于， 两点，直线， 分别与轴交于点， ．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）以为直径的圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面平面ABCD，，，，点E在BC上，．

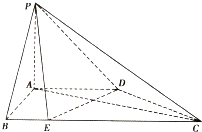
    （1）求证：平面平面PAC；

    （2）若直线PE与平面PAC所成的角的正弦值为，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：(a>b>0)的左.右顶点分别为A，B，离心率为，点P为椭圆上一点．

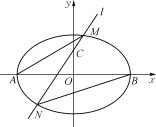
    (1) 求椭圆C的标准方程；

    (2) 如图，过点C(0，1)且斜率大于1的直线l与椭圆交于M，N两点，记直线AM的斜率为k1，直线BN的斜率为k2，若k1＝2k2，求直线l斜率的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若方程有四个不等的实数根，则的取值范围是（ ）

    A.B.或

    C.或D.或

    查看答案和解析>>

    同步练习册答案