
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次实验,得到数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 关于
关于 的线性回归方程
的线性回归方程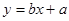 ;
; ,
, ,
,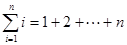
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”
知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和
频率分布直方图.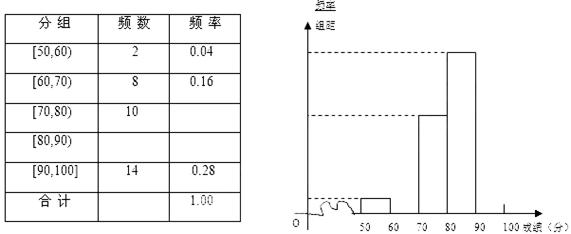
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在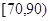 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
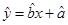 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。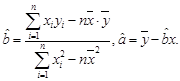 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件?2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
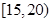 | 24 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 |  | 1 |

 及图中
及图中 的值;
的值; 内的人数;
内的人数; 内的概率.
内的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
 ;(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.(相关公式:
;(3)试根据(2)求出的线性回归方程,预测记忆力为9的同学的判断力.(相关公式: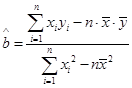 ,
, )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(Ⅲ)在这次测试中,学生跳绳次数的中位数、众数各是是多少?(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x | 2 | 4 | 5 | 6 | 8 |
| 销售额y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某地区的一种传染病与饮用水的调查表:
| | 得病 | 不得病 | 合计 |
| 干净水 | 52 | 466 | 518 |
| 不干净水 | 94 | 218 | 312 |
| 合计 | 146 | 684 | 830 |
 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com