
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为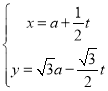 (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点、
).在以坐标原点为极点、![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
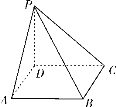
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,
中,![]() 为矩形,
为矩形,![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
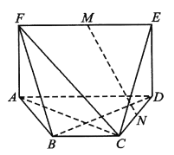
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求多面体
,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
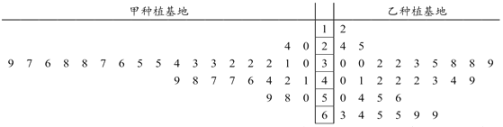
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,①已知点
中,①已知点![]() ,直线
,直线![]() :
:![]() ,动点
,动点![]() 满足到点
满足到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ;②已知圆
;②已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 为圆
为圆![]() 的切线,记点
的切线,记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,动点
,动点![]() 满足
满足![]() ;③点
;③点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,且
轴上运动,且![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)在①,②,③这三个条件中任选一个,求动点![]() 的轨迹方程;
的轨迹方程;
(2)记(1)中的轨迹为![]() ,经过点
,经过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴相交于点
轴相交于点![]() ,求点
,求点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,
,![]() ,记数列
,记数列![]() 的前n项和是
的前n项和是![]() ,则( )
,则( )
A.若数列![]() 是常数列,则
是常数列,则![]()
B.若![]() ,则数列
,则数列![]() 单调递减
单调递减
C.若![]() ,则
,则![]()
D.若![]() ,任取
,任取![]() 中的9项
中的9项![]() 构成数列
构成数列![]() 的子数列
的子数列![]() ,则
,则![]() 不全是单调数列
不全是单调数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P经过点![]() ,并且与圆
,并且与圆![]() 相切.
相切.
(Ⅰ)求圆心P的轨迹C的方程;
(Ⅱ)O是坐标原点,过点![]() 的直线
的直线![]() 与C交于A,B两点,在C上是否存在点Q,使得四边形
与C交于A,B两点,在C上是否存在点Q,使得四边形![]() 是平行四边形?
是平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com