
分析 (1)利用至少抽到1个编号为1的小球的概率为$\frac{4}{5}$,建立方程,即可求编号为1的小球个数;
(2)确定一次从袋中随机抽取3个球,抽到编号为3的小球的概率,即可求出恰有2次抽到编号为3的小球的概率;
(3)确定随机变量X所有可能的取值,求出相应的概率,即可求出随机变量X的分布列与数学期望.
解答 解:(1)设编号为1的小球个数为n(n∈N+,n≤4),
∵至少抽到1个编号为1的小球的概率为$\frac{4}{5}$,
∴1-$\frac{{C}_{6-n}^{2}}{{C}_{6}^{2}}$=$\frac{4}{5}$,
∴n=3或8(舍去),
∴编号为1的小球个数为3;
(2)一次从袋中随机抽取3个球,抽到编号为3的小球的概率为P=$\frac{{C}_{5}^{2}}{{C}_{6}^{3}}$=$\frac{1}{2}$
∴有放回的抽取3次,恰有2次抽到编号为3的小球的概率为${C}_{3}^{2}•(\frac{1}{2})^{2}•\frac{1}{2}$=$\frac{3}{8}$;
(3)随机变量X所有可能的取值为1,2,3,则
P(X=1)=$\frac{{C}_{3}^{3}}{{C}_{6}^{3}}$=$\frac{1}{20}$;P(X=2)=$\frac{{C}_{2}^{1}{C}_{3}^{2}+{C}_{2}^{2}{C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$;P(X=3)=$\frac{{C}_{5}^{2}}{{C}_{6}^{3}}$=$\frac{10}{20}$
∴随机变量X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{10}{20}$ |
点评 本题考查概率的计算,考查离散型随机变量的分布列与数学期望,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
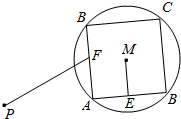 如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )
如图,已知圆M的半径为2,点P与圆心M的距离为4,正方形ABCD是圆M的内接四边形,E,F是边AB,AD的中点,当正方形ABCD绕圆心M转动时,$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是( )| A. | [-2,2] | B. | [-2$\sqrt{2}$,2$\sqrt{2}$] | C. | [-4,4] | D. | [-4$\sqrt{2}$,4$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -6 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,ex<0 | |
| B. | 若a,b∈R,a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| C. | 命题p:?x∈R,f(x)≥0,则?p:?x0∈R,f(x)<0 | |
| D. | 命题“在△ABC中,若$\overrightarrow{AB}•\overrightarrow{BC}$<0,则△ABC为钝角三角形的逆命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com