
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽子3个,肉粽子2个,白粽子5个,这三种粽子的外观完全相同,从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设ξ表示取到的豆沙粽子个数,求ξ的分布列.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】
(1)先求出基本事件总数,再求出三种粽子各取到1个包含的基本事件个数,由此能求出三种粽子各取到1个的概率.
(2)设ξ表示取到的豆沙粽子个数,由题意得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列.
(1)设一盘中装有10个粽子,其中豆沙粽子3个,肉粽子2个,白粽子5个,
这三种粽子的外观完全相同,从中任意选取3个,
基本事件总数n![]() 120,
120,
三种粽子各取到1个包含的基本事件个数m![]() 30,
30,
∴三种粽子各取到1个的概率p![]() .
.
(2)设ξ表示取到的豆沙粽子个数,
由题意得ξ的可能取值为0,1,2,3,
P(ξ=0)![]() ,
,
P(ξ=1)![]() ,
,
P(ξ=2)![]() ,
,
P(ξ=3)![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
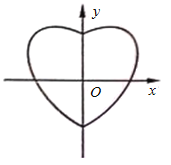
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面几种说法:
①相等向量的坐标相同;
②若向量![]() 满足
满足![]() ,则
,则![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共线的四点,则“
是不共线的四点,则“![]() ”是“四边形
”是“四边形![]() 为平行四边形”的充要条件;
为平行四边形”的充要条件;
④![]() 的充要条件是
的充要条件是![]() 且
且![]() .
.
其中正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
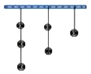
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() ,给出下列命题:①“
,给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件;其中真命题的个数是( )
”的必要条件;其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有限集合S中元素的个数记做![]() ,设A,B都为有限集合,给出下列命题:
,设A,B都为有限集合,给出下列命题:
①![]() 的充要条件是
的充要条件是![]()
②![]() 的必要不充分条件是
的必要不充分条件是![]()
③![]() 的充分不必要条件是
的充分不必要条件是![]()
④![]() 的充要条件是
的充要条件是![]()
其中,真命题有( )
A.①②③B.①②C.②③D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com