
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(1)求椭圆![]() 长半轴长;
长半轴长;
(2)求![]() 最大值;
最大值;
(3)若直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 的面积与
的面积与![]() 的面积的乘积为定值.
的面积的乘积为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)根据椭圆过点![]() 得到
得到![]() 的值,结合离心率得到
的值,结合离心率得到![]() 的值,得到答案;
的值,得到答案;
(2)根据椭圆的几何特点,得到![]() 与
与![]() 轴重合时,
轴重合时,![]() 最大,从而得到答案;
最大,从而得到答案;
(3)根据对称性设![]() ,
,![]() ,表示出直线
,表示出直线![]() 、
、![]() ,得到
,得到![]() 、
、![]() 坐标,从而表示出
坐标,从而表示出![]() 的面积与
的面积与![]() 的面积,得到面积的乘积为定值.
的面积,得到面积的乘积为定值.
(1)因为椭圆过点![]() ,所以
,所以![]() ,
,
因为离心率为![]() ,所以
,所以![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以求椭圆![]() 长半轴长为
长半轴长为![]() ;
;
(2)由(1)可得椭圆的标准方程为![]() ,
,
过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,
,
可知当![]() 为长轴时候最长,
为长轴时候最长,
此时![]() .
.
(3)由对称性可知![]() 、
、![]() 两点关于原点对称,
两点关于原点对称,
所以设![]() ,则
,则![]() ,
,
不妨假设![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得到
,得到![]() ,
,
所以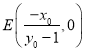 ,
,
同理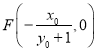 ,
,
所以![]() ,
,![]()
所以![]()
![]()
![]()
而![]() 在椭圆上,所以
在椭圆上,所以![]() ,即
,即![]() ,
,
所以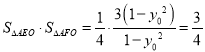 .
.
所以![]() 的面积与
的面积与![]() 的面积的乘积为定值
的面积的乘积为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】甲乙二人轮流掷一枚质地均匀的骰子,甲先掷.规定:若甲掷出1点,则由甲继续掷,否则下一次由乙掷;若乙掷出3点,则由乙继续掷,否则下一次由甲掷,两人始终按此规则进行.记第![]() 次由甲掷的概率为
次由甲掷的概率为![]() ,则
,则![]() ______,
______,![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正四面体ABCD中,M,N分别为棱AB和CD的中点,一个平面分别与棱BC,BD,AD,AC交于E,F,G,H,且MN⊥平面EFGH.给出下列六个结论:①AC⊥BD,②AB//平面EFGH,③平面ABC⊥平面EFGH,④四边形EFGH的周长为定值;⑤四边形EFGH的面积有最大值;⑥四边形EFGH一定是矩形,其中,所有正确结论的序号是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知一个动点M在圆![]() 上移动,它与定点
上移动,它与定点![]() 所连线段的中点为P.
所连线段的中点为P.
(1)求点P的轨迹方程.
(2)过定点![]() 的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
的直线与点P的轨迹交于A,B两点,求弦AB的中点C的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD为梯形,AB∥CD,∠DAB=90°,BDD1B1为矩形,平面BDD1B1⊥平面ABCD,又AB=AD=BB1=1,CD=2.
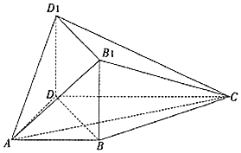
(1)证明:CB1⊥AD1;
(2)求B1到平面ACD1的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com