
分析 (1)n≥2时,Sn=$\frac{3}{2}$(an-1),Sn-1=$\frac{3}{2}$(an-1-1),两式相减即可得出an=3an-1,即可得出an.
(2)利用“分组求和法”即可得出Tn.
解答 解:(1)n≥2时,Sn=$\frac{3}{2}$(an-1),Sn-1=$\frac{3}{2}$(an-1-1),
两式相减得an=$\frac{3}{2}$(an-an-1),
∴an=3an-1,又S1=$\frac{3}{2}$(a1-1),得到a1=3,
∴an=3n,
又数列{bn}满足bn+1=$\frac{1}{4}$bn,且b1=4.
∴bn=42-n.
(2)由(1)可知:cn=an+log2bn=3n+log242-n=3n+log224-2n=3n+(4-2n).
Tn=2+31+0+32+(-2)+33+…+(4-2n)+3n=(31+32+33+…+3n)+(2+0-2-4…+4-2n)=$\frac{3(1-{3}^{n})}{1-3}$+4n-n(n+1)=$\frac{3}{2}({3}^{n}-1)$+3n-n2.
点评 本题考查了递推式的应用、“分组求和”、等比数列、等差数列的前n和公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (4,-4) | B. | (6,8) | C. | (5,12) | D. | (3,11) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(2,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
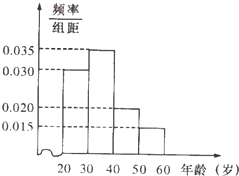 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 27 | 16 |
| [30,40) | 28 | 18 |
| [40,50) | 26 | 9 |
| [50,60] | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com