
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]() +
+ ![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
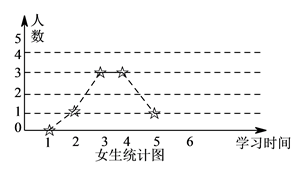
(I)已知该校有 ![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足 ![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于 ![]() 小时的学生中选取
小时的学生中选取 ![]() 人,设选到的男生人数为
人,设选到的男生人数为 ![]() ,求随机变量
,求随机变量 ![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差 ![]() 与女生学习时间方差
与女生学习时间方差 ![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数λ>0,设函数f(x)=eλx﹣ ![]() .
.
(Ⅰ)当λ=1时,求函数g(x)=f(x)+lnx﹣x的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C满足sin2A+sin(A﹣B+C)=sin(C﹣A﹣B)+ ![]() ,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
,面积S满足1≤S≤2,记a,b,c分别为A,B,C所对的边,在下列不等式一定成立的是( )
A.bc(b+c)>8
B.ab(a+b)>16 ![]()
C.6≤abc≤12
D.12≤abc≤24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期和单调递增区间;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对角为x,试求x的范围及此时函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F2(1,0),点H(2,
=1(a>b>0)的右焦点为F2(1,0),点H(2, ![]() )在椭圆上.
)在椭圆上.
(1)求椭圆的方程;
(2)点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点,求证:△PF2Q的周长是定值.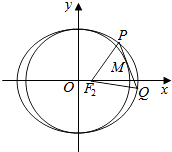
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+ ![]() 中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+
中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+ ![]() =x求得x=
=x求得x= ![]() .类比上述过程,则
.类比上述过程,则 ![]() =( )
=( )
A.3
B.![]()
C.6
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,焦点在x轴的椭圆,离心率e= ![]() ,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).
,且过点A(﹣2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线y=1反射后交椭圆于Q点(Q点与P点不重合).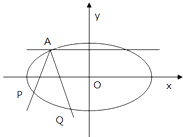
(1)求椭圆标准方程;
(2)求证:直线PQ的斜率为定值;
(3)求△OPQ的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.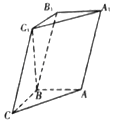
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)E是棱CC1所在直线上的一点,若二面角A﹣B1E﹣B的正弦值为 ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com