
【题目】某大学餐饮中心为了了解新生的饮食习惯,在某学院大一年级100名学生中进行了抽样调查,发现喜欢甜品的占70%.这100名学生中南方学生共80人.南方学生中有20人不喜欢甜品.
(1)完成下列![]() 列联表:
列联表:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | |||
北方学生 | |||
合计 |
(2)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(3)已知在被调查的南方学生中有6名数学系的学生,其中2名不喜欢甜品;有5名物理系的学生,其中1名不喜欢甜品.现从这两个系的学生中,各随机抽取2人,记抽出的4人中不喜欢甜品的人数为X,求X的分布列和数学期望.
附: .
.
【答案】(1)详见解析;(2)有95%的把握认为“南方学生和北方学生在选甜品的饮食习惯方面有差异”;(3)分布列详见解析,数学期望为![]() .
.
【解析】
(1)由南方学生共80人,南方学生中有20人不喜欢甜品,总人数为100,喜欢甜点的占70%,即可填表;
(2)根据列联表中的数据求出![]() 的值,然后再结合临界值表中的数据可得结论;
的值,然后再结合临界值表中的数据可得结论;
(3)根据离散型随机变量的概率公式计算分布列和数学期望.
解:(1)
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(2)由题意,
![]() ,
,
∴有95%的把握认为“南方学生和北方学生在选甜品的饮食习惯方面有差异”.
(3)X的所有可能取值为0,1,2,3,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以X的数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】现有![]() ,
,![]() ,…,
,…,![]() 这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计
这5个球队进行单循环比赛(全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场).当比赛进行到一定阶段时,统计![]() ,
,![]() ,
,![]() ,
,![]() 这4个球队已经赛过的场数分别为:
这4个球队已经赛过的场数分别为:![]() 队4场,
队4场,![]() 队3场,
队3场, ![]() 队2场,
队2场,![]() 队1场,则
队1场,则![]() 队比赛过的场数为( )
队比赛过的场数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为不同的两点,直线
为不同的两点,直线![]() ,下列命题正确的有( ).
,下列命题正确的有( ).
①不论![]() 为何值,点
为何值,点![]() 都不在直线
都不在直线![]() 上;
上;
②若![]() ,则过点
,则过点![]() 的直线与直线
的直线与直线![]() 平行;
平行;
③若![]() ,则直线
,则直线![]() 经过
经过![]() 的中点;
的中点;
④若![]() ,则点
,则点![]() 在直线
在直线![]() 的同侧且直线
的同侧且直线![]() 与线段
与线段![]() 的延长线相交.
的延长线相交.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,
, ![]() 的离心率
的离心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
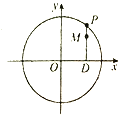
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com