
【题目】设集合A=[0, ![]() ),B=[
),B=[ ![]() ,1],函数f (x)=
,1],函数f (x)= 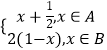 ,若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
,若x0∈A,且f[f (x0)]∈A,则x0的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[0, ![]() ]
]
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响。对近六年的年宣传费
(单位:万元)的影响。对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() 。对上述数据作了初步处理,得到相关的值如下表:
。对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好。现从这6年中任选2年,记其中选到效益良好年的数量为
内时认为该年效益良好。现从这6年中任选2年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望。(其中
的分布列和期望。(其中![]() 为自然对数的底数,
为自然对数的底数, ![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足 ![]()
![]() =0,
=0, ![]() =2
=2 ![]() .
.
(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为k的直线 l与圆x2+y2=1相切,直线 l与(1)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且 ![]() ≤
≤ ![]()
![]() ≤
≤ ![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为{x|x∈R,且x≠0},对定义域内的任意x1、x2,都有f(x1·x2)=f(x1)+f(x2),且当x>1时,f(x)>0.
(1)求证:f(x)是偶函数;
(2)求证:f(x)在(0,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=﹣x0 , 则称x0是f(x)的一个“次不动点”,也称f(x)在区间D上存在次不动点.若函数f(x)=ax2﹣3x﹣a+ ![]() 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an= ![]() ,若从{an}中提取一个公比为q的等比数列{
,若从{an}中提取一个公比为q的等比数列{ ![]() },其中k1=1,且k1<k2<…<kn , kn∈N* , 则满足条件的最小q的值为 .
},其中k1=1,且k1<k2<…<kn , kn∈N* , 则满足条件的最小q的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com