
分析 (1)由$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列,利用等差数列的性质列出关系式,整理即可得到结果;
(2)由等差数列的性质列出关系式,表示出b,再利用余弦定理表示出cosB,把表示出的b代入并利用基本不等式判断cosB的正负,即可做出判断.
解答 解:(1)∵a,b,c任意两边长均不相等,若$\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列,
∴$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$>$\frac{2}{\sqrt{ac}}$,即$\frac{1}{b}$>$\frac{1}{\sqrt{ac}}$,
则$\sqrt{\frac{c}{b}}$>$\sqrt{\frac{b}{a}}$;
(2)∵$\frac{2}{b}$=$\frac{1}{a}$+$\frac{1}{c}$,
∴b=$\frac{2ac}{a+c}$,
由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-(\frac{2ac}{a+c})^{2}}{2ac}$=$\frac{({a}^{2}+{c}^{2})(a+c)^{2}-4{a}^{2}{c}^{2}}{2ac(a+c)^{2}}$≥$\frac{2ac•4ac-4{a}^{2}{c}^{2}}{2ac(a+c)^{2}}$=$\frac{4ac-2ac}{(a+c)^{2}}$=$\frac{2ac}{(a+c)^{2}}$>0,
则B不可能为钝角.
点评 此题考查了余弦定理,以及数列的应用,熟练掌握余弦定理是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
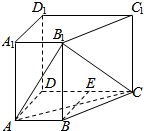 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com