
【题目】已知函数![]() ,其中数列
,其中数列![]() 是公比为
是公比为![]() 的等比数列,数列
的等比数列,数列![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若![]() ,
,![]() ,分别写出数列
,分别写出数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
(2)若![]() 是奇函数,且
是奇函数,且![]() ,求
,求![]() ;
;
(3)若函数![]() 的图像关于点
的图像关于点![]() 对称,且当
对称,且当![]() 时,函数
时,函数![]() 取得最小值,求
取得最小值,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】在甲地,随着人们生活水平的不断提高,进入电影院看电影逐渐成为老百姓的一种娱乐方式.我们把习惯进入电影院看电影的人简称为“有习惯”的人,否则称为“无习惯的人”.某电影院在甲地随机调查了100位年龄在15岁到75岁的市民,他们的年龄的频数分布和“有习惯”的人数如下表:

(1)以年龄45岁为分界点,请根据100个样本数据完成下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“有习惯”的人与年龄有关;
的把握认为“有习惯”的人与年龄有关;

(2)已知甲地从15岁到75岁的市民大约有11万人,以频率估计概率,若每张电影票定价为![]() 元
元![]() ,则在“有习惯”的人中约有
,则在“有习惯”的人中约有![]() 的人会买票看电影(
的人会买票看电影(![]() 为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
参考公式:![]() ,其中
,其中![]() .
.
参考临界值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
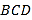
(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,并且图象关于y轴对称,当x≤-1时,y=f(x)的图象是经过点(-2,0)与(-1,1)的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(1,1)的一段抛物线.
(1)试求出函数f(x)的表达式,作出其图象;
(2)根据图象说出函数的单调区间,以及在每一个单调区间上函数是增函数还是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(1)若函数![]() 是奇函数,试证明:对任意的
是奇函数,试证明:对任意的![]() ,恒有
,恒有![]() ;
;
(2)若对于![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值是3,试求实数
上的最大值是3,试求实数![]() 的值;
的值;
(3)设![]() 且
且![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() ?如果存在,请求出
?如果存在,请求出![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,D,E分别为
,D,E分别为![]() 的中点,点F为线段
的中点,点F为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.


(1)求二面角![]()
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com