
【题目】1,4,9,16……这些数可以用图1中的点阵表示,古希腊毕达哥拉斯学派将其称为正方形数,记第![]() 个数为
个数为![]() .在图2的杨辉三角中,第
.在图2的杨辉三角中,第![]() 行是
行是![]() 展开式的二项式系数
展开式的二项式系数![]() ,
,![]() ,…,
,…,![]() ,记杨辉三角的前
,记杨辉三角的前![]() 行所有数之和为
行所有数之和为![]() .
.

(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以教材第97页B组第3题的函数![]() 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数![]() 是偶函数;
是偶函数;
②同学乙发现:对于任意的![]() 都有
都有![]() ;
;
③同学丙发现:对于任意的![]() ,都有
,都有![]() ;
;
④同学丁发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,总满足
,总满足![]() .
.
其中所有正确研究成果的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为![]() ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为![]() .
.
(1)求甲队分别以![]() ,
,![]() 获胜的概率;
获胜的概率;
(2)设![]() 表示决出冠军时比赛的场数,求
表示决出冠军时比赛的场数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
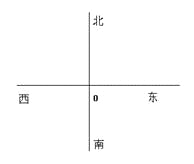
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图所示的某种容器的体积为![]() ,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为
,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为![]() .圆锥的高为
.圆锥的高为![]() ,母线与底面所成的角为
,母线与底面所成的角为![]() ;圆柱的高为
;圆柱的高为![]() ,已知圆柱底面的造价为
,已知圆柱底面的造价为![]() 元
元![]() ,圆柱侧面造价为
,圆柱侧面造价为![]() 元
元![]() ,圆锥侧面造价为
,圆锥侧面造价为![]()
![]() 元
元![]() .
.
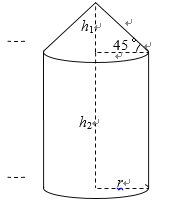
(1)将圆柱的高![]() 表示为底面半径
表示为底面半径![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)当容器造价最低时,圆柱的底面半径![]() 为多少?
为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com