
分析 利用分段函数性质、对数性质、运算法则和换底公式求解.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{log_4}x,\;x>0\\{3^x},\;x≤0\end{array}\right.$,
∴f(2)+f(8)=log42+log48=$\frac{lg2}{lg4}+\frac{lg8}{lg4}$=$\frac{1}{2}+\frac{3}{2}$=2,
f($\frac{1}{16}$)=$lo{g}_{4}\frac{1}{16}$=-2,
$f[f(\frac{1}{16})]$=f(-2)=3-2=$\frac{1}{9}$.
故答案为:2,$\frac{1}{9}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意对数性质、运算法则和换底公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
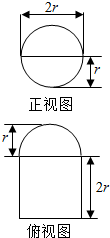 圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.
圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 8 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com