
已知集合
A和集合B各含12个元素,A∩B含有4个元素,试求同时满足下面两个条件的集合的个数.(1)
(2)C
∩A≠Φ(Φ表示空集).|
解析:本题与“集合 A有12个元素,集合B有8个元素,且A∩B≠Φ,求在集合A∪B中取3个元素,其中至少含有A的1个元素构成的集合C的个数”等价.解法一: (直接法)∵card(A∪B)=card(A)+card(B)-card(A∩B),∴ card(A∪B)=12+12-4=20.满足题设条件的集合 C可划分三类:第一类: A中取1个元素,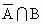 中取2个元素有 中取2个元素有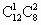 ; ;
第二类: A中取2个元素,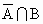 中取1个元素有 中取1个元素有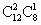 ; ;
第三类: A中取3个元素,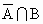 中取0个元素有 中取0个元素有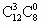 . .
∴满足题设要求的集合 C的个数为
解法二: (间接法)∵A∪B中共有20个元素,从20个元素中取3个元素的方法数为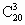 ,所取元素属于B而不属于A的取法有 ,所取元素属于B而不属于A的取法有 种, 种,
∴符合题意的集合 C有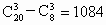 个. 个. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知集合A和集合B各含有12个元素,A∩B含4个元素,试求同时满足下面两个条件的集合C的个数:(1)C A B
,且C中含有3个元素;(2)
B
,且C中含有3个元素;(2) (
( 表示空集)。
表示空集)。
查看答案和解析>>
科目:高中数学 来源:1986年全国统一高考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com