
(200
6北京宣武模拟)如下图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD.(1)
求异面直线DA与BC所成的角;(2)
求证:平面DAE⊥平面CEA;(3)
求面EDA与面ABC所成二面角的大小.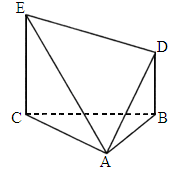
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:044
(2006
北京宣武模拟)已知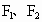 分别是双曲线
分别是双曲线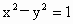 的两个焦点,O为坐标原点,圆O是以
的两个焦点,O为坐标原点,圆O是以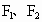 为直径的圆,直线l∶y=kx+b与圆O相切,并与双曲线交于A、B两点.
为直径的圆,直线l∶y=kx+b与圆O相切,并与双曲线交于A、B两点.
(1)
根据条件求出b和k满足的关系式;(2)
向量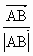 在向量
在向量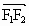 方向的投影是p,当
方向的投影是p,当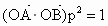 时,求直线l的方程;
时,求直线l的方程;
(3)
当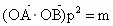 ,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).
,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).查看答案和解析>>
科目:高中数学 来源: 题型:013
(2006
北京宣武模拟)已知R为实数集,Q为有理数集,设函数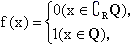 则
则
[
]A
.函数y=f(x)的图象是两条平行直线B
.函数y=f(x)是奇函数C
.函数f[f(x)]恒等于0D
.函数f[f(x)]的导函数恒等于0查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com