
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
【答案】
(1)证明:∵O,M分别为AB,VA的中点,
∴OM∥VB,
∵VB平面MOC,OM平面MOC,
∴VB∥平面MOC
(2)证明:∵AC=BC,O为AB的中点,
∴OC⊥AB,
∵平面VAB⊥平面ABC,OC平面ABC,
∴OC⊥平面VAB,
∵OC平面MOC,
∴平面MOC⊥平面VAB
(3)解:在等腰直角三角形ACB中,AC=BC= ![]() ,∴AB=2,OC=1,
,∴AB=2,OC=1,
∴S△VAB= ![]() ,
,
∵OC⊥平面VAB,
∴VC﹣VAB= ![]() S△VAB=
S△VAB= ![]() ,
,
∴VV﹣ABC=VC﹣VAB= ![]()
【解析】(1)利用三角形的中位线得出OM∥VB,利用线面平行的判定定理证明VB∥平面MOC;(2)证明:OC⊥平面VAB,即可证明平面MOC⊥平面VAB(3)利用等体积法求三棱锥V﹣ABC的体积.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 上有一个动点
上有一个动点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,动点
轴,动点![]() 在
在![]() 上,且满足
上,且满足![]() (
(![]() 为坐标原点),记点
为坐标原点),记点![]() 的轨迹为
的轨迹为![]() .
.
(I)求曲线![]() 的方程;
的方程;
(II)若直线![]() 是曲线
是曲线![]() 的一条切线,当点
的一条切线,当点![]() 到直线
到直线![]() 的距离最短时,求直线
的距离最短时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况, ![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用网络外卖 | 偶尔或不用网络外卖 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)根据表中数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和Sn=an﹣1,则关于数列{an}的下列说法中,正确的个数有( )
①一定是等比数列,但不可能是等差数列
②一定是等差数列,但不可能是等比数列
③可能是等比数列,也可能是等差数列
④可能既不是等差数列,又不是等比数列
⑤可能既是等差数列,又是等比数列.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an=an﹣1+3(n≥2,n∈N*),数列{bn}满足bn= ![]() ,n∈N* , 则
,n∈N* , 则 ![]() (b1+b2+…+bn) .
(b1+b2+…+bn) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2
,∠ACB=30°,PA=PC=5,PB=4,AB=BC=2 ![]() ,∠ACB=30°.
,∠ACB=30°. 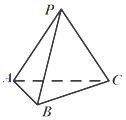
(1)求证:AC⊥PB;
(2)求三棱锥P﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+|x|)﹣ ![]() ,则使得f(x)>f(2x﹣1)成立的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的取值范围是( )
A.(﹣∞, ![]() )∪(1,+∞)?
)∪(1,+∞)?
B.( ![]() ,1)
,1)
C.(- ![]() ,
, ![]() )?
)?
D.(﹣∞,﹣ ![]() ,)
,) ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() ,
, ![]() 满足|
满足| ![]() |=1,|
|=1,| ![]() |=2.
|=2.
(1)若 ![]() 与
与 ![]() 的夹角θ=120°,求|
的夹角θ=120°,求| ![]() +
+ ![]() |的值;
|的值;
(2)若(k ![]() +
+ ![]() )⊥(k
)⊥(k ![]() ﹣
﹣ ![]() ),求实数k的值.
),求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com