
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名中学生的笔试成绩,按成绩分组,得到的频率分布表如下所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | ① | 0.350 |
第3组 | [170,175) | 30 | ② |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185) | 10 | 0.100 |
合计 | 100 | 1.00 |
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图,并从频率分布直方图中求出中位数(中位数保留整数);

(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,从这6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率.
【答案】(1)见解析,中位数172;(2)![]() .
.
【解析】
(1)由频率分布直方图能求出第2组的频数,第3组的频率,从而完成频率分布直方图.
(2)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,利用列举法能出从这六位同学中抽取两位同学,第4组至少有一名学生被考官A面试的概率.
(1)①由题可知,第2组的频数为0.35×100=35人,②第3组的频率为![]() =0.300,
=0.300,
频率分布直方图如图所示,
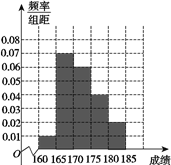
160至165的频率为0.05,165至170的频率为0.35,170至175的频率为0.30
故知中位数在170至175之间,设为x,
则(x﹣170)×0.06+0.40=0.5,
解得x=172,故中位数为172.
(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生进入第二轮面试,每组抽取的人数分别为:
第3组:![]() ×6=3人,
×6=3人,
第4组:![]() ×6=2人,
×6=2人,
第5组:![]() ×6=1人,
×6=1人,
所以第3、4、5组分别抽取3人、2人、1人进入第二轮面试.
设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的1位同学为C1,
则从这六位同学中抽取两位同学有
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1),共15种,
其中第4组的2位同学B1,B2中至少有一位同学入选的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C1),(B2,C1),共有9种,所以第4组至少有一名学生被考官A面试的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,四个顶点构成的菱形的面积是4,圆M:(x+1)2+y2=r2(0<r<1).过椭圆C的上顶点A作圆M的两条切线分别与椭圆C相交于B,D两点(不同于点A),直线AB,AD的斜率分别为k1 , k2 .
,四个顶点构成的菱形的面积是4,圆M:(x+1)2+y2=r2(0<r<1).过椭圆C的上顶点A作圆M的两条切线分别与椭圆C相交于B,D两点(不同于点A),直线AB,AD的斜率分别为k1 , k2 .
(1)求椭圆C的方程;
(2)当r变化时,①求k1k2的值;②试问直线BD是否过某个定点?若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为![]() .现已知相距
.现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为
两家化工厂(污染源)的污染强度分别为![]() ,它们连线上任意一点
,它们连线上任意一点![]() 处(异于
处(异于![]() 两点)的污染指数
两点)的污染指数![]() 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设![]() .
.
(1)试将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,且
,且![]() 时,
时,![]() 取得最小值,试求
取得最小值,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(0,3),与双曲线
=1(a>b>0)过点A(0,3),与双曲线 ![]() =1有相同的焦点
=1有相同的焦点
(1)求椭圆C的方程;
(2)过A点作两条相互垂直的直线,分别交椭圆C于P,Q两点,则PQ是否过定点?若是,求出定点的坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线C经过定点P(3,![]() ),它的一个焦点为F(1,0),对应于该焦点的准线为x=-1,斜率为2的直线
),它的一个焦点为F(1,0),对应于该焦点的准线为x=-1,斜率为2的直线![]() 交圆锥曲线C于A、B两点,且 AB =
交圆锥曲线C于A、B两点,且 AB =![]() ,求圆锥曲线C和直线
,求圆锥曲线C和直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦晚会期间,高三二班的学生准备了6 个参赛节目,其中有 2 个舞蹈节目,2 个小品节目,2个歌曲节目,要求歌曲节目一定排在首尾,另外2个舞蹈节目一定要排在一起,则这 6 个节目的不同编排种数为
A. 48 B. 36 C. 24 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,∠BAC= ![]() ,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=
,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP= ![]() .
.
(Ⅰ)若AB=3,求PC;
(Ⅱ)求 ![]()
![]() 的取值范围.
的取值范围.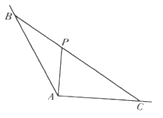
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线城市 | 一线城市 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
|
|
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() ,
,
参照附表,得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C. 有99%以上的把握认为“生育意愿与城市级别有关”
D. 有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为 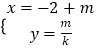 ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(Ⅰ)写出C的普通方程;
(Ⅱ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com