
| A. | $13\sqrt{6}π$ | B. | $27\sqrt{6}π$ | C. | 27$\sqrt{7}$π | D. | 7$\sqrt{6}$π |
分析 设出球的半径,小圆半径,通过已知条件求出球的半径,即可求球的体积.
解答 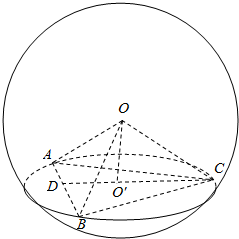 解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,
则OO′⊥面ABC.在Rt△ACD中,cosA=$\frac{1}{3}$,则sinA=$\frac{2\sqrt{2}}{3}$,
在△ABC中,由正弦定理得$\frac{6}{sinA}$=2R,R=$\frac{9\sqrt{2}}{4}$,即O′C=$\frac{9\sqrt{2}}{4}$.
在Rt△OCO′中,由题意得r2-$\frac{1}{4}$r2=($\frac{9\sqrt{2}}{4}$)2,得r=$\frac{3\sqrt{6}}{2}$.
球的体积=$\frac{4}{3}$πr3=27$\sqrt{6}$π.
故选:B.
点评 本题考查球的体积的求法以及正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | Π7<Π8 | B. | Π15<Π16 | C. | Π13>1 | D. | Π14>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (1)(2) | B. | (1)(2)( 3) | C. | (1)(2)(4) | D. | (1)(2)(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com