
| A. | [-$\frac{3}{4}$,0) | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,1] |
分析 先根据条件画出图形,由得到直线的距离公式求得O到直线AB的距离d=$\frac{1}{2}$.得到$\frac{1}{2}$≤|$\overrightarrow{OC}$|<1,把$\overrightarrow{CM}$•$\overrightarrow{CN}$转化为含有$|\overrightarrow{OC}|$的代数式得答案.
解答 解:如图,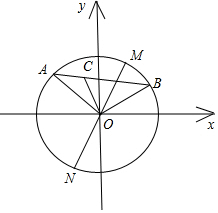
∵OA=OB=1,∠AOB=120°;
∴O到直线AB的距离d=$\frac{1}{2}$.
∴$\frac{1}{2}$≤|$\overrightarrow{OC}$|<1,
则$\overrightarrow{CM}$•$\overrightarrow{CN}$=($\overrightarrow{OM}-\overrightarrow{OC}$)•($\overrightarrow{ON}-\overrightarrow{OC}$)
=$\overrightarrow{OM}•\overrightarrow{ON}$-($\overrightarrow{OM}+\overrightarrow{ON}$)•$\overrightarrow{OC}$+$|\overrightarrow{OC}{|}^{2}$
=-1+$|\overrightarrow{OC}{|}^{2}$.
∴-$\frac{3}{4}$≤$\overrightarrow{CM}•\overrightarrow{CN}$<0.
∴$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围为[-$\frac{3}{4}$,0),
故选:A.
点评 本题平面向量的数量积运算,考查数形结合解题的方法及数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,1)∪(1,+∞) | C. | (1,+∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .. | B. | $\frac{9}{8}$ | C. | $\frac{8}{9}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
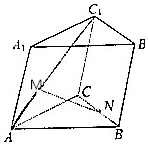 如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).
如图所示,已知斜三棱柱ABC-A1B1C1,点M,N分别在AC1和BC上,且满足$\overrightarrow{AM}$=k$\overrightarrow{A{C}_{1}}$,$\overrightarrow{BN}$=k$\overrightarrow{BC}$(0≤k≤1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
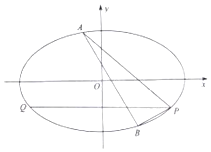 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com