
【题目】已知点![]() 是圆
是圆![]() :
:![]() 上任意一点,点
上任意一点,点![]() 与点
与点![]() 关于原点对称,线段
关于原点对称,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于
交于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() 使以
使以![]() 为直径的圆恒过这个点?若存在,求出点
为直径的圆恒过这个点?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1) ![]() (2) 在
(2) 在![]() 轴上存在定点
轴上存在定点![]() ,使以
,使以![]() 为直径的圆恒过这个点.
为直径的圆恒过这个点.
【解析】试题分析:(1)由圆的方程求出F1、F2的坐标,结合题意可得点M的轨迹C为以F1,F2为焦点的椭圆,并求得a,c的值,再由隐含条件求得b,则椭圆方程可求;
(2)直线l的方程可设为![]() ,设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求出A,B横坐标的和与积,假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,可得
,设A(x1,y1),B(x2,y2),联立直线方程与椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求出A,B横坐标的和与积,假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,可得![]() 即
即![]() .利用向量的坐标运算即可求得m值,即定点Q得坐标.
.利用向量的坐标运算即可求得m值,即定点Q得坐标.
试题解析:
解:(1)由题意得![]() ,
,
∴点![]() 的轨迹
的轨迹![]() 为以
为以![]() 为焦点的椭圆
为焦点的椭圆
∵![]() ,
,
∴![]()
∴点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率存在时,可设其方程为
的斜率存在时,可设其方程为![]() ,设
,设![]()
联立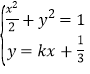 可得
可得![]() ,
,
由求根公式可得![]()
假设在![]() 轴上存在定点
轴上存在定点![]() ,使以
,使以![]() 为直径的圆恒过这个点,
为直径的圆恒过这个点,
则![]() 即
即![]()
∵![]()
![]() ,
,
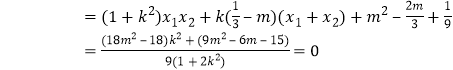 ,
,
由![]() 解得
解得![]()
∴在![]() 轴上存在定点
轴上存在定点![]() ,使以
,使以![]() 为直径的圆恒过这个点.
为直径的圆恒过这个点.
当直线![]() 的斜率不存在时,经检验可知也满足以
的斜率不存在时,经检验可知也满足以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.
因此在![]() 轴上存在定点
轴上存在定点![]() ,使以
,使以![]() 为直径的圆恒过这个点.
为直径的圆恒过这个点.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
, ![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(3)在(2)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识增强环保意识,某校从理工类专业甲班抽取60人,从文史类乙班抽取50人参加环保知识测试 附:k2= ![]() ,n=a+b+c+d
,n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(1)根据题目条件完成下面2×2列联表,并据此判断你是否有99%的把握认为环保知识与专业有关
优秀 | 非优秀 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(2)为参加上级举办的环保知识竞赛,学校举办预选赛,预选赛答卷满分100分,优秀的同学得60分以上通过预选,非优秀的同学得80分以上通过预选,若每位同学得60分以上的概率为 ![]() ,得80分以上的概率为
,得80分以上的概率为 ![]() ,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,求X的分布列及期望E(X).
,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,求X的分布列及期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年12月4日0时起郑州市实施机动车单双号限行,新能源汽车不在限行范围内,某人为了出行方便,准备购买某能源汽车.假设购车费用为14.4万元,每年应交付保险费、充电费等其他费用共0.9万元,汽车的保养维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,…,依等差数列逐年递增.
(1)设使用![]() 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为![]() ,试写出
,试写出![]() 的表达式;
的表达式;
(2)问这种新能源汽车使用多少年报废最合算(即该车使用多少年平均费用最少),年平均费用的最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a﹣1)x+(a2﹣5)=0}
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上, ![]() 是
是![]() 的中点,证明:
的中点,证明: ![]() ;
;
(2)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程.
(2)已知直线l平行于直线4x+3y-7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln2x-2aln(ex)+3,x∈[e-1,e2]
(1)当a=1时,求函数f(x)的值域;
(2)若f(x)≤-alnx+4恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com