
【题目】已知点P是圆F1:(x+1)2+y2=16上任意一点(F1是圆心),点F2与点F1关于原点对称.线段PF2的中垂线m分别与PF1、PF2交于M、N两点.
(1)求点M的轨迹C的方程;
(2)直线l经过F2 , 与抛物线y2=4x交于A1 , A2两点,与C交于B1 , B2两点.当以B1B2为直径的圆经过F1时,求|A1A2|.
【答案】
(1)解:由题意得,F1(﹣1,0),F2(1,0),圆F1的半径为4,且|MF2|=|MP|,
从而|MF1|+|MF2|=|MF1|+|MP|=|PF1|=4>|F1F2|,)
∴点M的轨迹是以F1,F2为焦点的椭圆,
其中长轴2a=4,得到a=2,焦距2c=2,
则短半轴b= ![]() ,
,
椭圆方程为: ![]()
(2)解:当直线l 与x轴垂直时,B1(1, ![]() ),B2(1,﹣
),B2(1,﹣ ![]() ),又F1(﹣1,0),
),又F1(﹣1,0),
此时 ![]() ,所以以B1B2为直径的圆不经过F1.不满足条件.
,所以以B1B2为直径的圆不经过F1.不满足条件.
当直线l 不与x轴垂直时,设L:y=k(x﹣1)
由 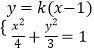 即(3+4k2)x2﹣8k2x+4k2﹣12=0,
即(3+4k2)x2﹣8k2x+4k2﹣12=0,
因为焦点在椭圆内部,所以恒有两个交点.
设B1(x1,y1),B2(x2,y2),则:x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
因为以B1B2为直径的圆经过F1,所以 ![]() ,又F1(﹣1,0)
,又F1(﹣1,0)
所以(﹣1﹣x1)(﹣1﹣x2)+y1y2=0,即(1+k2)x1x2+(1﹣k2)(x1+x2)+1+k2=0
所以解得k2= ![]() ,
,
由 ![]() 得k2x2﹣(2k2+4)x+k2=0
得k2x2﹣(2k2+4)x+k2=0
因为直线l 与抛物线有两个交点,所以k≠0,
设A1(x3,y3),A2(x4,y4),则:x3+x4= ![]() =2+
=2+ ![]() ,x3x4=1
,x3x4=1
所以|A1A2|=x3+x4+p=2+ ![]() +2=
+2= ![]() .
.
【解析】(1)先确定F1、F2的坐标,再根据线段PF2的中垂线与与PF1、PF2交于M点,结合椭圆的定义,可得点M的轨迹是以F1、F2为焦点的椭圆,从而可得点M的轨迹C的方程;(2)当直线l与x轴垂直时,B1(1, ![]() ),B2(1,﹣
),B2(1,﹣ ![]() ),不满足条件,当直线l不与x轴垂直时,设直线l的方程为:y=k(x﹣1),由
),不满足条件,当直线l不与x轴垂直时,设直线l的方程为:y=k(x﹣1),由  ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判别式、韦达定理、圆的性质、弦长公式能求出|A1A2|.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判别式、韦达定理、圆的性质、弦长公式能求出|A1A2|.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(﹣3,1),
=(﹣3,1), ![]() =(1,﹣2),
=(1,﹣2), ![]() =
= ![]() +k
+k ![]() (k∈R).
(k∈R).
(1)若 ![]() 与向量2
与向量2 ![]() ﹣
﹣ ![]() 垂直,求实数k的值;
垂直,求实数k的值;
(2)若向量 ![]() =(1,﹣1),且
=(1,﹣1),且 ![]() 与向量k
与向量k ![]() +
+ ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为( ) 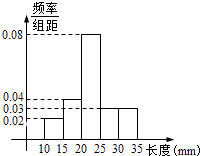
A.20
B.25
C.22.5
D.22.75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)对于定义域内的任意x都满足 ![]() ,则称f(x)具有性质M.
,则称f(x)具有性质M.
(1)很明显,函数 ![]() (x∈(0,+∞)具有性质M;请证明
(x∈(0,+∞)具有性质M;请证明 ![]() (x∈(0,+∞)在(0,1)上是减函数,在(1,+∞)上是增函数.
(x∈(0,+∞)在(0,1)上是减函数,在(1,+∞)上是增函数.
(2)已知函数g(x)=|lnx|,点A(1,0),直线y=t(t>0)与g(x)的图象相交于B、C两点(B在左边),验证函数g(x)具有性质M并证明|AB|<|AC|.
(3)已知函数 ![]() ,是否存在正数m,n,k,当h(x)的定义域为[m,n]时,其值域为[km,kn],若存在,求k的范围,若不存在,请说明理由.
,是否存在正数m,n,k,当h(x)的定义域为[m,n]时,其值域为[km,kn],若存在,求k的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , P是椭圆上一点,|PF1|=λ|PF2|(
=1(a>b>0)的左、右焦点分别为F1、F2 , P是椭圆上一点,|PF1|=λ|PF2|( ![]() ≤λ≤2),∠F1PF2=
≤λ≤2),∠F1PF2= ![]() ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,C上一点(3,m)到焦点的距离为5.
(1)求C的方程;
(2)过F作直线l,交C于A、B两点,若线段AB中点的纵坐标为﹣1,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值. 【答案】解:由
的值. 【答案】解:由 ![]() π<x<
π<x< ![]() π,得
π,得 ![]() π<x+
π<x+ ![]() <2π,
<2π,
又cos ![]() =
= ![]() ,∴sin
,∴sin ![]() =﹣
=﹣ ![]() ;
;
∴cosx=cos ![]() =cos
=cos ![]() cos
cos ![]() +sin
+sin ![]() sin
sin ![]() =﹣
=﹣ ![]() ,
,
从而sinx=﹣ ![]() ,tanx=7;
,tanx=7;
故原式= ![]() ;
;
(1)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ![]() ,M为AB的中点.
,M为AB的中点. 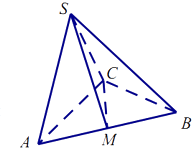
(1)求证:AC⊥SB;
(2)求二面角S﹣CM﹣A的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com