Question

一个几何体是由圆柱ADD₁A₁和三棱锥E-ABC组合而成，点A、B、C在圆O的圆周上，其正（主）视图、侧（左）视图的面积分别为10和12，如图所示，其中EA⊥平面ABC，AB⊥AC，AB=AC，AE=2．

（1）求证：AC⊥BD；

（2）求二面角A-BD-C的平面角的大小．

Answer 1

分析：方法一（几何法）（1）由已知中EA⊥平面ABC，由线面垂直的性质可得ED⊥AC，结合AC⊥AB，由线面垂直的判定定理可得AC⊥平面EBD，再由线面垂直的性质得到AC⊥BD；
（2）由A、B、C在圆O的圆周上，且AB⊥AC，所以BC为圆O的直径，又由几何体正（主）视图、侧（左）视图的面积分别为10和12，我们易构造r，h的方程组，求出r，h的值后，结合（1）的结论，可得∠AHC为二面角A-BD-C的平面角，解Rt△BAD，即可得到二面角A-BD-C的平面角的大小．
方法二（向量法）（1）以点D为原点，DD₁、DE所在的射线分别为x轴、z轴建立如图的空间直角坐标系，分别求出AC，BD的方向向量，由两向量的数量积为0，即可得到AC⊥BD；
（2）分别求出平面ABD与平面BCD的法向量，代入向量夹角公式，即可得到二面角A-BD-C的平面角的大小．

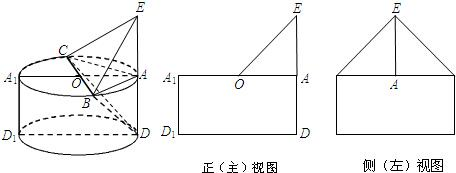
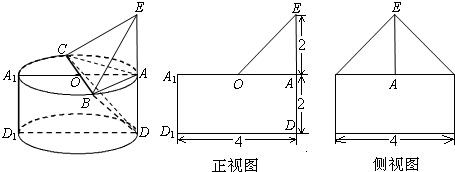
解答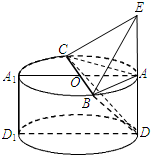：方法一（几何法）：
证明：（1）因为EA⊥平面ABC，AC?平面ABC，所以EA⊥AC，即ED⊥AC．
又因为AC⊥AB，AB∩ED=A，所以AC⊥平面EBD．
因为BD?平面EBD，所以AC⊥BD．（4分）
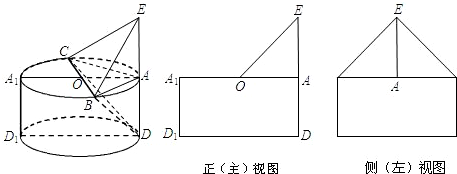
解：（2）因为点A、B、C在圆O的圆周上，且AB⊥AC，所以BC为圆O的直径．
设圆O的半径为r，圆柱高为h，根据正（主）视图、侧（左）视图的面积可得，

2rh+ 1 2 r×2=10 2rh+ 1 2 ×2r×2=12.

（6分）
解得

r=2 h=2.

所以BC=4，AB=AC=2

2

．（7分）
过点C作CH⊥BD于点H，连接AH，
由（1）知，AC⊥BD，AC∩CH=C，所以BD⊥平面ACH．
因为AH?平面ACH，所以BD⊥AH．
所以∠AHC为二面角A-BD-C的平面角．（9分）
由（1）知，AC⊥平面ABD，AH?平面ABD，
所以AC⊥AH，即△CAH为直角三角形．
在Rt△BAD中，AB=2

2

，AD=2，则BD=

AB2+AD2

=2

3

．
由AB×AD=BD×AH，解得AH=

2 6

3

．
因为tan∠AHC=

AC

AH

=

3

．（13分）
所以∠AHC=60°．
所以二面角A-BD-C的平面角大小为60°．（14分）
方法二（向量法）：
证明：（1）因为点A、B、C在圆O的圆周上，且AB⊥AC，所以BC为圆O的直径．
设圆O的半径为r，圆柱高为h，根据正（主）视图、侧（左）视图的面积可得，

2rh+ 1 2 r×2=10 2rh+ 1 2 ×2r×2=12.

（2分）
解得

r=2 h=2.

所以BC=4，AB=AC=2

2

．
以点D为原点，DD₁、DE所在的射线分别为x轴、z轴建立如图的空间直角坐标系
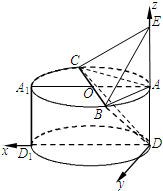
D-xyz，则D（0，0，0），D₁（4，0，0），A（0，0，2），B（2，2，2），C（2，-2，2），

AC

=(2，-2，0)，

DB

=(2，2，2)．
因为

AC

•

DB

=(2，-2，0)•(2，2，2)=0，
所以

AC

⊥

DB

．
所以AC⊥BD．（9分）
解：（2）设n=（x，y，z）是平面BCD的法向量，因为

BC

=(0，-4，0)，
所以

n• BC =0 n• DB =0.

即

-4y=0 2x+2y+2z=0.

取z=-1，则n=（1，0，-1）是平面BCD的一个法向量．（11分）
由（1）知，AC⊥BD，又AC⊥AB，AB∩BD=B，所以AC⊥平面ABD．
所以

AC

=(2，-2，0)是平面ABD的一个法向量．（12分）
因为cos?n，

AC

＞=

n• AC

|n|•| AC |

=

2

2 ×2 2

=

1

2

，
所以?n，

AC

＞=60°．
而?n，

AC

＞等于二面角A-BD-C的平面角，
所以二面角A-BD-C的平面角大小为60°．（14分）

点评：本题考查的知识点是二面角的平面角及求示，直线与平面垂直的性质，其中方法一中的关键是熟练掌握线面垂直与线线垂直的转化，结合二面角的定义，确定∠AHC为二面角A-BD-C的平面角，方法二的关键是建立空间坐标系，将直线的垂直及二面角问题转化为向量夹角问题．