
【题目】设函数f(x)=ax2﹣(a+1)x+1.
(1)若不等式f(x)<mx的解集为{x|1<x<2},求实数a、m的值;
(2)解不等式f(x)<0.
【答案】
(1)解:∵f(x)=ax2﹣(a+1)x+1,
∴不等式f(x)<mx等价于ax2﹣(a+m+1)x+1<0,
依题意知不等式ax2﹣(a+m+1)x+1<0的解集为{x|1<x<2},
∴a>0且1和2为方程ax2﹣(a+m+1)x+1=0的两根,
∴  ,
,
解得 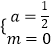 ,
,
∴实数a、m的值分别为a=1、m=0
(2)解:不等式f(x)<0可化为(ax﹣1)(x﹣1)<0,
(ⅰ)当a=0时,不等式f(x)<0等价于﹣x+1<0,解得x>1,
故原不等式的解集为{x|x>1},
(ⅱ)当a>0时,不等式f(x)<0等价于 ![]() ,
,
①当0<a<1时 ![]() ,不等式
,不等式 ![]() 的解集为
的解集为 ![]() ,
,
即原不等式的解集为 ![]() ,
,
②当a=1时,不等式 ![]() 的解集为φ,
的解集为φ,
即原不等式的解集为φ,
③当a>1时 ![]() ,不等式
,不等式 ![]() 的解集为
的解集为 ![]() ,
,
即原不等式的解集为 ![]() ,
,
(ⅲ)当a<0时,不等式f(x)<0等价于 ![]() ,
,
∵a<0,
∴ ![]() ,
,
∴不等式 ![]() 的解集为{x|x<
的解集为{x|x< ![]() 或x>1},
或x>1},
即原不等式的解集为{x|x< ![]() 或x>1},
或x>1},
综上所述,当a>1时不等式f(x)<0的解集为 ![]() ,
,
当a=1时不等式f(x)<0的解集为φ,
当0<a<1时不等式f(x)<0的解集为 ![]() ,
,
当a=0时不等式f(x)<0的解集为{x|x>1},
当a<0时不等式f(x)<0的解集为为{x|x< ![]() 或x>1}
或x>1}
【解析】(1)根据一元二次不等式的解集,利用根与系数的关系,即可求出实数a、m的值;(2)不等式化为(ax﹣1)(x﹣1)<0,讨论a=0和a>0、a<0时,求出不等式f(x)<0的解集即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减,以及对解一元二次不等式的理解,了解求一元二次不等式
上递减,以及对解一元二次不等式的理解,了解求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足 ![]() ,
, ![]() ,n∈N* .
,n∈N* .
(1)求证:数列 ![]() 为等比数列;
为等比数列;
(2)是否存在互不相等的正整数m,s,t,使m,s,t成等差数列,且am﹣1,as﹣1,at﹣1成等比数列?如果存在,求出所有符合条件的m,s,t;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:
分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
频数 | 1 | 2 | 6 | 7 | 3 | 1 |
分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为( )
A.10%
B.20%
C.30%
D.40%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校1200名高三年级学生参加了一次数学测验(满分为100分),为了分析这次数学测验的成绩,从这1200人的数学成绩中随机抽出200人的成绩绘制成如下的统计表,请根据表中提供的信息解决下列问题;
(1)求a、b、c的值;
(2)如果从这1200名学生中随机取一人,试估计这名学生该次数学测验及格的概率p(注:60分及60分以上为及格);
(3)试估计这次数学测验的年级平均分.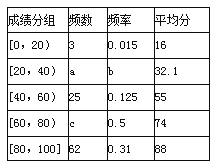
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张老师给学生出了一道题,“试写一个程序框图,计算S=1+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
”.发现同学们有如下几种做法,其中有一个是错误的,这个错误的做法是( )
A.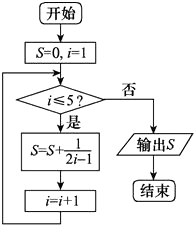
B.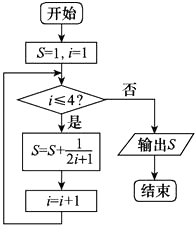
C.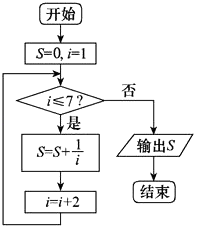
D.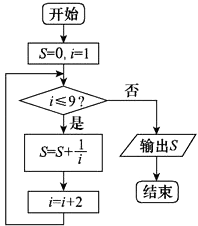
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三文科分为五个班.高三数学测试后,随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生,求分数不小于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 【2017四川宜宾二诊】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知点
中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为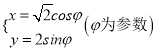 .以原点为极点,
.以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为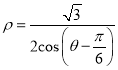 .
.
(Ⅰ)判断点![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= ![]() AA1 , D是棱AA1的中点.
AA1 , D是棱AA1的中点.
(Ⅰ)证明:平面BDC1⊥平面BDC
(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比.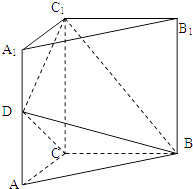
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com