
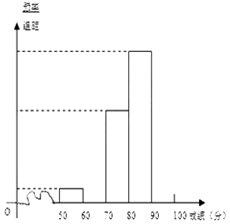
 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.| 分 组 | 频 数 | 频 率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.2 |
| [80,90) | 16 | 0.32 |
| [90,100] | 14 | 0.28 |
| 合 计 | 50 | 1.00 |
分析 (1)先填写完整频率分布表,由此能补全频率分布直方图.
(2)设中位数为x,利用频率分布直方图列出方程,给求出中位数.
(3)由题意知样本分数在[60,70)有8人,样本分数在[80,90)有16人,用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,则抽取的分数在[60,70)和[80,90)的人数分别为2人和4人.记分数在[60,70)为a1,a2在[80,90)的为b1,b2,b3,b4.由此利用列举法能求出2人分数都在[80,90)的概率.
解答 解:(1)填写频率分布表中的空格,如下表: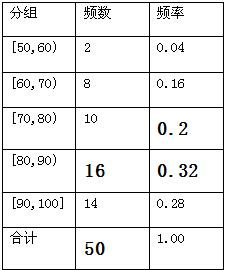
补全频率分布直方图,如下图: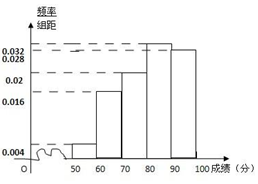
故答案为:0.2,16,0.32,50.…(5分)
(2)设中位数为x,依题意得0.04+0.16×6+0.2+0.032×(x-80)=0.5,
解得x=83.125. 所以中位数约为83.125.…(7分)
(3)由题意知样本分数在[60,70)有8人,样本分数在[80,90)有16人,
用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,
则抽取的分数在[60,70)和[80,90)的人数分别为2人和4人.
记分数在[60,70)为a1,a2在[80,90)的为b1,b2,b3,b4.
从已抽取的6人中任选两人的所有可能结果有15种,分别为:
$\begin{array}{l}\left\{{{a_1},{a_2}}\right\},\left\{{{a_1},{b_1}}\right\},\left\{{{a_1},{b_2}}\right\},\left\{{{a_1},{b_3}}\right\},\left\{{{a_1},{b_4}}\right\}\\ \left\{{{a_2},{b_1}}\right\},\left\{{{a_2},{b_2}}\right\},\left\{{{a_2},{b_3}}\right\},\left\{{{a_2},{b_4}}\right\}\\ \left\{{{b_1},{b_2}}\right\},\left\{{{b_1},{b_3}}\right\},\left\{{{b_1},{b_4}}\right\},\left\{{{b_2},{b_3}}\right\},\left\{{{b_2},{b_4}}\right\},\left\{{{b_3},{b_4}}\right\}\end{array}$.
设“2人分数都在[80,90)”为事件A,
则事件A包括{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}共6种.…(8分)
所以$P(A)=\frac{6}{15}=\frac{2}{5}$…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 104人 | B. | 108人 | C. | 112人 | D. | 120人 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有游戏一公平 | B. | 只有游戏二公平 | ||
| C. | 两个游戏都不公平 | D. | 两个游戏都公平 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | [1,2] | C. | (1,2] | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -2 | D. | 2$\sqrt{3}$-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
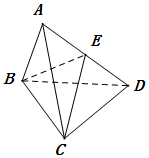 如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com