
【题目】如图,在三棱锥P﹣ABC中,AC=![]() BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
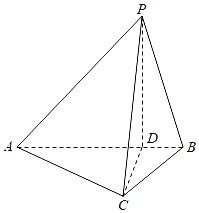
(1)求证:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)推导出AC⊥BC,CD⊥AD,PD⊥CD,从而CD⊥平面PAB,由此能证明平面PAB⊥平面PCD.
(2)以D为坐标原点,分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角P-AC-D的平面角的余弦值.
(1)证明:∵AC=![]() BC,AB=2BC,
BC,AB=2BC,
∴![]() ,
,
∴AB2=AC2+BC2,∴AC⊥BC,
在Rt△ABC中,由AC=![]() BC,得∠CAB=30°,
BC,得∠CAB=30°,
设BD=1,由AD=3BD,得AD=3,BC=2,AC=2![]() ,
,
在△ACD中,由余弦定理得CD2=AD2+AC2﹣2ADACcos30°=3,
∴CD=![]() ,
,
∴CD2+AD2=AC2,∴CD⊥AD,
∵PD⊥平面ABC,CD![]() 平面ABC,
平面ABC,
∴PD⊥CD,
又PD∩AD=D,∴CD⊥平面PAB,
又CD![]() 平面PCD,∴平面PAB⊥平面PCD.
平面PCD,∴平面PAB⊥平面PCD.
(2)解:∵PD⊥平面ABC,
∴PA与平面ABC所成角为∠PAD,即∠PAD=45°,
∴△PAD为等腰直角三角形,PD=AD,
由(1)得PD=AD=3,以D为坐标原点,
分别以DC,DB,DP所在直线为x,y,z轴,建立空间直角坐标系,
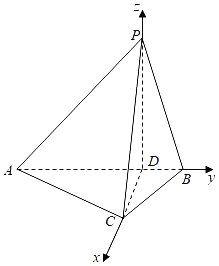
则D(0,0,0),C(![]() ,0,0),A(0,﹣3,0),P(0,0,3),
,0,0),A(0,﹣3,0),P(0,0,3),
![]() =(0,﹣3,﹣3),
=(0,﹣3,﹣3),![]() =(
=(![]() ),
),
则![]() =
=![]() =(0,0,3)是平面ACD的一个法向量,
=(0,0,3)是平面ACD的一个法向量,
设平面PAC的一个法向量![]() =(x,y,z),
=(x,y,z),
则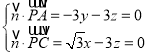 ,取x=
,取x=![]() ,得
,得![]() =(
=(![]() ,﹣1,1),
,﹣1,1),
设二面角P﹣AC﹣D的平面角为θ,
则cosθ=![]() =
=![]() ,
,
∴二面角P﹣AC﹣D的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交抛物线的弦长为2.
轴垂直的直线交抛物线的弦长为2.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 和点
和点![]() 为两定点,点
为两定点,点![]() 和点
和点![]() 为抛物线
为抛物线![]() 上的两动点,线段
上的两动点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
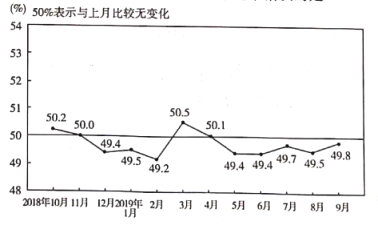
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且n、
,且n、![]() 、
、![]() 成等差数列,
成等差数列,![]() .
.
(1)证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 中去掉数列
中去掉数列![]() 的项后余下的项按原顺序组成数列
的项后余下的项按原顺序组成数列![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,且
,且![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与以线段
与以线段![]() 为直径的圆相交于
为直径的圆相交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
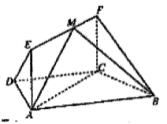
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,椭圆
两点,椭圆![]() 的右顶点为
的右顶点为![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,且定点
,且定点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com