【答案】
分析:(1)先确定正项等比数列的公比,可得a
n,利用n≥2时,b
n=S
n-S
n-1,可求b
n;
(2)由题意得:2
n≥5n-1+c对一切n∈N
*都成立,所以c≤2
n-5n+1对一切n∈N
*都成立,令d
n=2
n-5n+1,可得d
n+1-d
n,确定单调性,即可求得c的最大值;
(3)确定数列{c
n}的通项,即可求满足c
n>2012的最小正整数n的值.
解答:解:(1)正项等比数列{a
n}中,a
1=2,a
3=8,∴q=2,∴a
n=2•2
n-1=2
n.…(2分)
当n=1时,b
1=S
1=1;
当n≥2时,b
n=S
n-S
n-1=5n-1;
∴b
1也满足b
n=5n-1.
综上,b
n=5n-1.…(4分)
(2)由题意得:2
n≥5n-1+c对一切n∈N
*都成立,
所以,c≤2
n-5n+1对一切n∈N
*都成立,
令d
n=2
n-5n+1,所以d
n+1-d
n=2
n-5,…(7分)
当n≤2时,d
n+1<d
n,{d
n}为递减数列,即d
1>d
2>d
3;
当n≥3时,d
n+1>d
n,{d
n}为递增数列,即d
3<d
4<d
5<…(9分)
所以d
n最小值为d
3=-6,
所以c≤-6,即c的最大值为-6..…(11分)
(3)
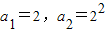
,
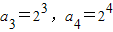
,…
b
1=4,b
2=9,b
3=14,b
2=19…
∴数列{a
n}与{b
n}中相同的项按从小到大的顺序排成一列为数列{c
n},即
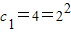
,
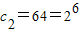
,
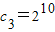
,
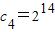
,…
∴
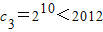
,
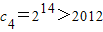
,
所以满足c
n>2012的最小正整数n的值为4.…(16分)
点评:本题考查等差数列与等比数列的通项,考查数列的单调性,考查恒成立问题,考查学生分析解决问题,难度较大,综合性强.

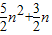 .
.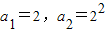 ,
,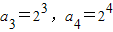 ,…
,…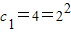 ,
,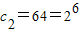 ,
,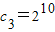 ,
,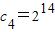 ,…
,…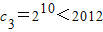 ,
,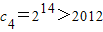 ,
,

 名校课堂系列答案
名校课堂系列答案