
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为4π,且对x∈R,有f(x)≤f(
)的最小正周期为4π,且对x∈R,有f(x)≤f( ![]() )成立,则关于函数f(x)的下列说法中正确的是( )
)成立,则关于函数f(x)的下列说法中正确的是( )
①φ= ![]()
②函数f(x)在区间[﹣π,π]上递减;
③把g(x)=sin ![]() 的图象向左平移
的图象向左平移 ![]() 得到f(x)的图象;
得到f(x)的图象;
④函数f(x+ ![]() )是偶函数.
)是偶函数.
A.①③
B.①②
C.②③④
D.①④
【答案】A
【解析】解:函数f(x)=sin(ωx+φ)(ω>0)的最小正周期为4π,
∴T= ![]() =4π,∴ω=
=4π,∴ω= ![]() ;
;
又对x∈R,有f(x)≤f( ![]() )成立,
)成立,
∴x= ![]() 时,函数f(x)取得最大值,
时,函数f(x)取得最大值,
∴ ![]() ×
× ![]() +φ=
+φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
又|φ|< ![]() ,∴φ=
,∴φ= ![]() ,①正确;
,①正确;
∴f(x)=sin( ![]() x+
x+ ![]() ),
),
当x∈[﹣π,π]时, ![]() x∈[﹣
x∈[﹣ ![]() ,
, ![]() ],
],
![]() x+
x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],函数f(x)不是单调递减函数,②错误;
],函数f(x)不是单调递减函数,②错误;
把g(x)=sin ![]() 的图象向左平移
的图象向左平移 ![]() ,得y=sin
,得y=sin ![]() (x+
(x+ ![]() )=sin(
)=sin( ![]() x+
x+ ![]() )的图象,
)的图象,
即为f(x)的图象,③正确;
函数f(x+ ![]() )=sin[
)=sin[ ![]() (x+
(x+ ![]() )+
)+ ![]() ]=sin(
]=sin( ![]() x+
x+ ![]() ),它不是偶函数,④错误.
),它不是偶函数,④错误.
综上,正确的命题是①③.
故选:A.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知A是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若
=1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若 ![]() =λ
=λ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |+|
|+| ![]() |=8,则双曲线的标准方程为( )
|=8,则双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.![]() ﹣y2=1
﹣y2=1
C.![]() =1
=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 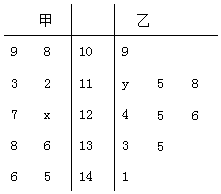
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2+ ![]() 的图象经过点(2,3),a为常数.
的图象经过点(2,3),a为常数.
(1)求a的值和函数f(x)的定义域;
(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱ABC﹣A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
(Ⅰ)求证:A1B∥平面B1DC;
(Ⅱ)求二面角D﹣B1C﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体A﹣BCD中,AB=CD=10,AC=BD=2 ![]() ,AD=BC=2
,AD=BC=2 ![]() ,则四面体A﹣BCD外接球的表面积为( )
,则四面体A﹣BCD外接球的表面积为( )
A.50π
B.100π
C.200π
D.300π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点. (I)求证:BE∥平面ACF;
(II)求平面BCF与平面BEF所成锐二面角的余弦角.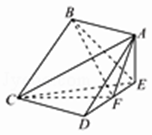
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com