Question

【题目】在平面直角坐标系xOy中，已知曲线C1的参数方程为 （φ为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4 cosθ．
（1）求C1与C2交点的直角坐标；
（2）已知曲线C3的参数方程为 （0≤α＜π，t为参数，且t≠0），C3与C1相交于点P，C2与C3相交于点Q，且|PQ|=8，求α的值．

Answer 1

【答案】
（1）解：曲线C1的参数方程为 （φ为参数），

消去参数可得：x2+（y﹣2）2=4．

曲线C2的极坐标方程为ρ=4 cosθ，即ρ2=4 ρcosθ，

化为直角坐标方程：x2+y2=4 x．

联立 ，

解得 ， ，

∴C1与C2交点的直角坐标分别为：（0，0）； ．

（2）解：曲线C3的参数方程为 （0≤α＜π，t为参数，且t≠0），

时，可得 ，代入方程：x2+（y﹣2）2=4，解得t=0，t=4．

代入：x2+y2=4 x，解得t=0，不满足|PQ|=8，舍去．

时，消去参数化为普通方程：y=xtanα，设k=tanα．

联立 ，解得 ， ，

可得P（0，0），或P ．

联立 ，解得 ， ，

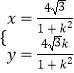可得Q（0，0），或Q ．

∵|PQ|=8，∴只能取P ，Q ．

∴ + =82，

化为： =0，解得k=﹣ ，

∴tanα=﹣ ，又0≤α＜π，解得α=

【解析】（1）曲线C1的参数方程为 （φ为参数），消去参数可得普通方程．曲线C2的极坐标方程为ρ=4 cosθ，即ρ2=4 ρcosθ，利用互化公式可得直角坐标方程，联立解出即可得出．（2）曲线C3的参数方程为 （0≤α＜π，t为参数，且t≠0）， 时，不满足|PQ|=8，舍去．
时，消去参数化为普通方程：y=xtanα，设k=tanα，即直线l的方程为：y=kx，分别与曲线C1 ， C2的方程联立解出交点P，Q的坐标，利用两点之间的距离公式即可得出．